填空题
已知M是椭圆$\frac {x}{9}$+$\frac {y}{5}$=1上一点，F$_1$，F$_2$是椭圆的两个焦点，I是△MF$_1$F$_2$的内心，延长MI交F$_1$F$_2$于N，则$\frac {|MI|}{|NI|}$等于．
填空题答案仅供参考
题目答案
$\frac {3}{2}$
您的答案
答案解析
分析：
由于三角形的内心是三个内角的平分线的交点，根据三角形内角平分线性质定理把所求的比值转化为三角形边长之间的比值关系来求解．
解答：
解：如图，连接IF$_1$，IF$_2$．在△MF$_1$I中，F$_1$I是∠MF$_1$N的角平分线，
根据三角形内角平分线性质定理，$\frac {|MI|}{|NI|}$=$\frac {|MF$_1$|}{|F$_1$N|}$，同理可得$\frac {|MI|}{|NI|}$=$\frac {|MF$_2$|}{|F$_2$N|}$，
∴$\frac {|MI|}{|NI|}$=$\frac {|MF$_1$|}{|F$_1$N|}$=$\frac {|MF$_2$|}{|F$_2$N|}$；
根据等比定理$\frac {|MI|}{|NI|}$=$\frac {|MF$_1$|+|MF$_2$|}{|F$_1$N|+|F$_2$N|}$=$\frac {2a}{2c}$=$\frac {2×3}{2×$\sqrt {9-5}$}$=$\frac {3}{2}$．
故答案为：$\frac {3}{2}$．
点评：
本题主要考查圆锥曲线的定义的应用，试题在平面几何中的三角形内角平分线性质定理、初中代数中的等比定理和圆锥曲线的定义之间进行了充分的交汇，在解决涉及到圆锥曲线上的点与焦点之间的关系的问题中，圆锥曲线的定义往往是解题的突破口．
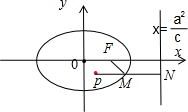解：由题意作图，