- 有理数(I)有理数(I)
- 正数与负数正数与负数
- 有理数的概念有理数的概念
- 有理数的分类有理数的分类
- 数轴数轴
- 相反数相反数
- 绝对值绝对值
- 绝对值非负性绝对值非负性
- 有理数比较大小有理数比较大小
- 有理数(II)有理数(II)
- 有理数的加法有理数的加法
- 减法及加减法混合运算减法及加减法混合运算
- 有理数凑整巧算有理数凑整巧算
- 有理数的乘法有理数的乘法
- 除法及乘除混合运算除法及乘除混合运算
- 有理数的四则混合运算有理数的四则混合运算
- 利用乘法分配律巧算利用乘法分配律巧算
- 有理数的乘方有理数的乘方
- 有理数的混合运算有理数的混合运算
- 科学记数法与近似数科学记数法与近似数
- 整式的加减整式的加减
- 用含字母的式子表示数用含字母的式子表示数
- 单项式单项式
- 多项式多项式
- 同类项同类项
- 整式的概念与方程综合整式的概念与方程综合
- 整式的加减整式的加减
- 整式化简之与某项无关整式化简之与某项无关
- 整式的化简与求值整式的化简与求值
- 利用特殊概念化简求值利用特殊概念化简求值
- 整体代入求值整体代入求值
- 加减两个已知式求未知式加减两个已知式求未知式
- 绝对值与平方的非负性绝对值与平方的非负性
- 绝对值的化简绝对值的化简
- 数轴上数的比较与运算数轴上数的比较与运算
- 数轴背景下的绝对值化简数轴背景下的绝对值化简
- 一元一次方程(I)一元一次方程(I)
- 一元一次方程一元一次方程
- 等式的性质等式的性质
- 合并同类项与移项合并同类项与移项
- 去括号去括号
- 去分母去分母
- 解分母是小数的一次方程解分母是小数的一次方程
- 与数字有关的一元一次方程与数字有关的一元一次方程
- 与工程有关的一元一次方程与工程有关的一元一次方程
- 与经济有关的一元一次方程与经济有关的一元一次方程
- 与行程有关的一元一次方程与行程有关的一元一次方程
- 方案决策问题方案决策问题
- 一元一次方程(II)一元一次方程(II)
- 简单的绝对值方程简单的绝对值方程
- 恒等式的概念恒等式的概念
- 恒等式之特值法恒等式之特值法
- 已知方程的解求参数已知方程的解求参数
- 同解问题同解问题
- 系数含参的一元一次方程系数含参的一元一次方程
- 整数解问题整数解问题
- 几何图形初步(I)几何图形初步(I)
- 展开图初步展开图初步
- 立方体的展开图立方体的展开图
- 立方体相对两面立方体相对两面
- 展开图进阶展开图进阶
- 旋转体旋转体
- 直线射线线段的概念直线射线线段的概念
- 几何作图初步几何作图初步
- 两点之间线段最短两点之间线段最短
- 与线段有关的简单计算与线段有关的简单计算
- 线段计算之多解问题线段计算之多解问题
- 线段计算之列方程线段计算之列方程
- 双中点模型双中点模型
- 几何图形初步(II)几何图形初步(II)
- 角的概念角的概念
- 角度换算角度换算
- 角度的四则运算角度的四则运算
- 余角和补角余角和补角
- 余角和补角之列方程余角和补角之列方程
- 方向角方向角
- 角度计算之三角板问题角度计算之三角板问题
- 角度计算之双直角模型角度计算之双直角模型
- 角度计算之角平分线角度计算之角平分线
- 双角平分线模型双角平分线模型
- 角度计算之列方程角度计算之列方程
- 相交线与平行线相交线与平行线
- 相交线相交线
- 垂直垂直
- 垂线段最短垂线段最短
- 角度计算之多解问题角度计算之多解问题
- 同位角、内错角、同旁内角同位角、内错角、同旁内角
- 平行线及其判定平行线及其判定
- 平行线的性质平行线的性质
- 与平行线有关的计算与平行线有关的计算
- 平行线之M模型平行线之M模型
- 命题与定理命题与定理
- 平移平移
- 实数实数
- 平方根平方根
- 立方根立方根
- 实数的概念实数的概念
- 根号几的估算根号几的估算
- 根号几的精确估算根号几的精确估算
- 平面直角坐标系平面直角坐标系
- 平面直角坐标系的概念平面直角坐标系的概念
- 坐标系不同区域点的特点坐标系不同区域点的特点
- 点到坐标轴的距离点到坐标轴的距离
- 坐标系中点的平移坐标系中点的平移
- 坐标系中图形的平移坐标系中图形的平移
- 已知两点确定第三点的坐标已知两点确定第三点的坐标
- 二元一次方程组二元一次方程组
- 二元一次方程组的概念二元一次方程组的概念
- 代入消元法代入消元法
- 加减消元法加减消元法
- 解复杂的二元一次方程组解复杂的二元一次方程组
- 概念中的二元一次方程组概念中的二元一次方程组
- 二元一次方程组实际问题二元一次方程组实际问题
- 三元一次方程组的解法三元一次方程组的解法
- 已知方程(组)的解求参数已知方程(组)的解求参数
- 解常数项含参的方程组解常数项含参的方程组
- 消元消元
- 不等式与不等式组不等式与不等式组
- 不等式不等式
- 不等式的性质不等式的性质
- 解一元一次不等式解一元一次不等式
- 解一元一次不等式组解一元一次不等式组
- 不等式与坐标系综合不等式与坐标系综合
- 不等式的应用不等式的应用
- 解常数项含参的不等式解常数项含参的不等式
- 解系数含参的不等式解系数含参的不等式
- 含参不等式组含参不等式组
- 含参方程与不等式综合含参方程与不等式综合
- 含参方程组与不等式综合含参方程组与不等式综合
- 数据的收集、整理与描述数据的收集、整理与描述
- 统计调查统计调查
- 常见统计图常见统计图
- 直方图直方图
- 利用关键数据补全图表利用关键数据补全图表
- 三角形(I)三角形(I)
- 三角形的三边关系三角形的三边关系
- 利用三边关系计数利用三边关系计数
- 三角形按边分类三角形按边分类
- 三角形中的线段三角形中的线段
- 三角形内角和定理三角形内角和定理
- 三角形内角和之列方程三角形内角和之列方程
- 三角形按角度分类三角形按角度分类
- 三角形中的双垂直模型三角形中的双垂直模型
- 三角形的外角三角形的外角
- 三角形与平行线综合三角形与平行线综合
- 高线角平分线综合高线角平分线综合
- 三角形(II)三角形(II)
- 多边形初步多边形初步
- 多边形的对角线多边形的对角线
- 多边形的内角和多边形的内角和
- 多边形的外角和多边形的外角和
- 多边形的内角和进阶多边形的内角和进阶
- “8”字形和“A”字形“8”字形和“A”字形
- 燕尾形燕尾形
- 内角平分线的交角内角平分线的交角
- 内外角平分线的交角内外角平分线的交角
- 全等三角形全等三角形
- 全等三角形的概念和性质全等三角形的概念和性质
- 全等三角形的判定(SSS)全等三角形的判定(SSS)
- 全等三角形的判定(SAS)全等三角形的判定(SAS)
- 全等三角形的判定(ASA)全等三角形的判定(ASA)
- 全等三角形的判定(HL)全等三角形的判定(HL)
- 全等三角形判定综合全等三角形判定综合
- 证了全等再说证了全等再说
- 角平分线的性质与判定角平分线的性质与判定
- 多次证明全等多次证明全等
- 三垂直模型三垂直模型
- 轴对称(I)轴对称(I)
- 轴对称基本概念和性质轴对称基本概念和性质
- 垂直平分线的性质与判定垂直平分线的性质与判定
- 垂直平分线作图问题垂直平分线作图问题
- 画轴对称图形画轴对称图形
- 将军饮马问题将军饮马问题
- 将军饮马问题的应用将军饮马问题的应用
- 多次对称确定最短路径多次对称确定最短路径
- 等边对等角等边对等角
- 等边对等角多解问题等边对等角多解问题
- 等腰三角形三线合一等腰三角形三线合一
- 等角对等边等角对等边
- 角平分线+平行角平分线+平行
- 轴对称(II)轴对称(II)
- 两圆一中垂两圆一中垂
- 等边三角形等边三角形
- 含30°角的直角三角形含30°角的直角三角形
- 等边三角形类弦图模型等边三角形类弦图模型
- 绕直角顶点转90度绕直角顶点转90度
- 等腰共顶点模型等腰共顶点模型
- 连接两点连接两点
- 倍长中线倍长中线
- 角平分线对称性之作垂线角平分线对称性之作垂线
- 角平分线对称性之翻折角平分线对称性之翻折
- 角平分线对称性之顺延角平分线对称性之顺延
- 截长补短截长补短
- 整式的乘法与因式分解(I)整式的乘法与因式分解(I)
- 同底数幂的乘法同底数幂的乘法
- 幂的乘方幂的乘方
- 积的乘方积的乘方
- 整式的乘法整式的乘法
- 同底数幂的除法同底数幂的除法
- 整式的除法整式的除法
- 平方差公式平方差公式
- 完全平方公式完全平方公式
- 已知完全平方式求系数已知完全平方式求系数
- 整式的化简与求值整式的化简与求值
- 整式乘法的系数问题整式乘法的系数问题
- 降次法求值降次法求值
- 整式的乘法与因式分解(II)整式的乘法与因式分解(II)
- 因式分解的概念因式分解的概念
- 提公因式法提公因式法
- 公式法之平方差公式公式法之平方差公式
- 公式法之完全平方公式公式法之完全平方公式
- 分组分解法分组分解法
- 首一的十字相乘法首一的十字相乘法
- 非首一的十字相乘法非首一的十字相乘法
- 已知x、y的积与和求代数式的值已知x、y的积与和求代数式的值
- 利用因式分解求值利用因式分解求值
- 利用配方求值利用配方求值
- 分式分式
- 分式的基本概念分式的基本概念
- 分式值为0分式值为0
- 分式的基本性质分式的基本性质
- 约分与通分约分与通分
- 分式的乘除分式的乘除
- 分式的加减分式的加减
- 分式的混合运算分式的混合运算
- 分式的化简与求值分式的化简与求值
- 整数指数幂整数指数幂
- 解分式方程解分式方程
- 解含参分式方程解含参分式方程
- 含参分式方程增根问题含参分式方程增根问题
- 行程问题行程问题
- 工程问题工程问题
- 其它问题其它问题
- 二次根式二次根式
- 二次根式的概念二次根式的概念
- 二次根式的非负性二次根式的非负性
- 去根号法则去根号法则
- 二次根式乘除法法则二次根式乘除法法则
- 最简二次根式最简二次根式
- 二次根式的乘除运算二次根式的乘除运算
- 同类二次根式同类二次根式
- 二次根式的加减二次根式的加减
- 二次根式综合运算二次根式综合运算
- 含字母的根式化简含字母的根式化简
- 被开方数的非负性被开方数的非负性
- 条件有理化条件有理化
- 分母有理化分母有理化
- 复合二次根式化简复合二次根式化简
- 勾股定理勾股定理
- 利用勾股定理求边长利用勾股定理求边长
- 勾股定理多解问题勾股定理多解问题
- 特殊直角三角形特殊直角三角形
- 利用勾股定理列方程利用勾股定理列方程
- 最短路径问题最短路径问题
- 网格与勾股定理网格与勾股定理
- 勾股定理的逆定理勾股定理的逆定理
- 平行四边形平行四边形
- 平行四边形的性质(一)平行四边形的性质(一)
- 平行四边形的性质(二)平行四边形的性质(二)
- 性质反过来就是判定性质反过来就是判定
- 平行且相等平行且相等
- 判定方法辨析判定方法辨析
- 三角形中位线的性质三角形中位线的性质
- 矩形的性质矩形的性质
- 斜边中线定理斜边中线定理
- 矩形的判定(一)矩形的判定(一)
- 矩形的判定(二)矩形的判定(二)
- 菱形的性质菱形的性质
- 菱形的判定(一)菱形的判定(一)
- 菱形的判定(二)菱形的判定(二)
- 正方形的性质正方形的性质
- 与正方形有关的旋转全等与正方形有关的旋转全等
- 中点四边形中点四边形
- 梯形梯形
- 梯形的概念梯形的概念
- 等腰梯形的性质等腰梯形的性质
- 等腰梯形的判定等腰梯形的判定
- 梯形辅助线之平移腰梯形辅助线之平移腰
- 梯形辅助线之作双高梯形辅助线之作双高
- 梯形的中位线梯形的中位线
- 四边形判定的辨析四边形判定的辨析
- 一次函数(I)一次函数(I)
- 变量与函数变量与函数
- 自变量取值范围及解析式自变量取值范围及解析式
- 函数的表示方式函数的表示方式
- 函数的解析式与图象函数的解析式与图象
- 实际问题的函数图象实际问题的函数图象
- 正比例函数的概念正比例函数的概念
- 正比例函数的图象与性质正比例函数的图象与性质
- 求正比例函数解析式求正比例函数解析式
- 从正比例到一次函数从正比例到一次函数
- 一次函数图象的性质一次函数图象的性质
- 补全直线上点坐标补全直线上点坐标
- 待定系数法求解析式待定系数法求解析式
- 一次函数的上下平移一次函数的上下平移
- 平行直线k相同平行直线k相同
- 一次函数(II)一次函数(II)
- 直线与直线的交点直线与直线的交点
- 一次函数与方程一次函数与方程
- 一次函数与不等式一次函数与不等式
- 一次函数与坐标轴围成的面积一次函数与坐标轴围成的面积
- 数据的分析数据的分析
- 平均数平均数
- 中位数和众数中位数和众数
- 方差和极差方差和极差
- 一元二次方程(I)一元二次方程(I)
- 一元二次方程一元二次方程
- 直接开平方法直接开平方法
- 配方法配方法
- 公式法公式法
- 根的判别式根的判别式
- 十字相乘法十字相乘法
- 提取公因式法提取公因式法
- 根与系数的关系根与系数的关系
- 增长率问题增长率问题
- 篱笆问题篱笆问题
- 草坪问题草坪问题
- 分式方程应用题分式方程应用题
- 一元二次方程(II)一元二次方程(II)
- 利用方程根的概念求值利用方程根的概念求值
- 已知一个根求另一个根已知一个根求另一个根
- 已知根的个数求参数已知根的个数求参数
- 证明方程恒有实根证明方程恒有实根
- 整数根之判别式整数根之判别式
- 整数根之直接求根整数根之直接求根
- 根与系数的关系的应用根与系数的关系的应用
- 两根的倒数和两根的倒数和
- 两根之差的绝对值两根之差的绝对值
- 二次函数(I)二次函数(I)
- 最简二次函数的图象最简二次函数的图象
- 顶点式二次函数的图象顶点式二次函数的图象
- 从一般式到顶点式从一般式到顶点式
- 二次函数图象上点的性质二次函数图象上点的性质
- 求抛物线与坐标轴的交点求抛物线与坐标轴的交点
- 求二次函数的解析式求二次函数的解析式
- 顶点式和交点式顶点式和交点式
- 二次函数图象的平移1二次函数图象的平移1
- 二次函数图象的平移2二次函数图象的平移2
- 二次函数图象的变换二次函数图象的变换
- 二次函数特定范围内的最值二次函数特定范围内的最值
- 二次函数最值之解析式含参二次函数最值之解析式含参
- 看图象求参数关系看图象求参数关系
- 二次函数(II)二次函数(II)
- 用函数观点解方程1用函数观点解方程1
- 用函数观点解方程2用函数观点解方程2
- 用函数观点解不等式用函数观点解不等式
- 图象分析大杂烩图象分析大杂烩
- 利用二次函数求点坐标利用二次函数求点坐标
- 定价问题定价问题
- 利用二次函数求最值利用二次函数求最值
- 直线与抛物线的交点直线与抛物线的交点
- 看图写范围看图写范围
- 抛物线与直线的垂直距离抛物线与直线的垂直距离
- 旋转旋转
- 图形的旋转图形的旋转
- 旋转图形的画法旋转图形的画法
- 中心对称的概念中心对称的概念
- 旋转特殊角度旋转特殊角度
- 互补四边形半角模型1互补四边形半角模型1
- 互补四边形半角模型2互补四边形半角模型2
- 等腰直角三角形半角模型等腰直角三角形半角模型
- 圆(I)圆(I)
- 圆的基本概念圆的基本概念
- 垂径定理垂径定理
- 弧、弦、圆心角弧、弦、圆心角
- 圆周角圆周角
- 等弧对等角等弧对等角
- 直径对直角直径对直角
- 圆内接四边形圆内接四边形
- 圆中的特殊角圆中的特殊角
- 圆(II)圆(II)
- 点和圆的位置关系点和圆的位置关系
- 三角形外接圆三角形外接圆
- 直线和圆的位置关系直线和圆的位置关系
- 切线判定定理切线判定定理
- 切线性质定理切线性质定理
- 切线长定理切线长定理
- 圆和圆的位置关系圆和圆的位置关系
- 正多边形和圆正多边形和圆
- 弧长弧长
- 扇形面积扇形面积
- 圆锥圆锥
- 概率初步概率初步
- 随机事件随机事件
- 概率概率
- 用列举法求概率用列举法求概率
- 用频率估计概率用频率估计概率
- 反比例函数反比例函数
- 反比例函数的概念反比例函数的概念
- 反比例函数的图象反比例函数的图象
- 反比例函数的解析式反比例函数的解析式
- k的几何意义k的几何意义
- 实际问题与反比例函数实际问题与反比例函数
- 求交点求交点
- 用函数的观点解不等式用函数的观点解不等式
- 特殊的面积问题特殊的面积问题
- 相似相似
- 相似的概念相似的概念
- 平行线分线段成比例平行线分线段成比例
- 相似三角形的判定相似三角形的判定
- 相似三角形的性质相似三角形的性质
- 相似三角形应用举例相似三角形应用举例
- 位似的概念位似的概念
- 反A模型反A模型
- 射影定理射影定理
- 旋转相似模型旋转相似模型
- 共线三等角模型共线三等角模型
- 三角形内接正方形三角形内接正方形
- 角平分线定理角平分线定理
- 锐角三角函数锐角三角函数
- 锐角三角函数锐角三角函数
- 特殊角的三角函数特殊角的三角函数
- 解直角三角形解直角三角形
- 解直角三角形的应用解直角三角形的应用
- 双直角三角形及其应用双直角三角形及其应用
- 设未知数解直角三角形设未知数解直角三角形
- 利用已知角构造直角三角形利用已知角构造直角三角形
- 解梯形解梯形
- 解四边形解四边形
- 作垂线解三角形之SSA作垂线解三角形之SSA
- 投影与视图投影与视图
- 投影投影
- 三视图的概念三视图的概念
- 立方体堆的三视图立方体堆的三视图
《特殊直角三角形》特殊直角三角形
1填空题
如图,修公路遇到一座山,于是要修一条隧道.为了加快施工进度,想在小山的另一侧同时施工.为了使山的另一侧的开挖点C在AB的延长线上,设想过C点作直线AB的垂线l,过点B作一直线(在山的旁边经过),与l相交于D点,经测量∠ABD=135°,BD=800米,则直线l上距离D点米的C处开挖.($\sqrt {2}$≈1.414,精确到1米)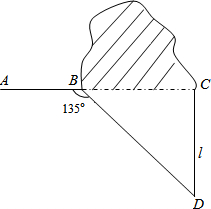
题目答案
您的答案
答案解析
分析:
首先证明△BCD是等腰直角三角形,再根据勾股定理可得CD_+BC_=BD_,然后再代入BD=800米进行计算即可.
解答:
解:∵CD⊥AC,
∴∠ACD=90°,
∵∠ABD=135°,
∴∠DBC=45°,
∴∠D=45°,
∴CB=CD,
在Rt△BCD中:CD_+BC_=BD_,
2CD_=800_,
CD=400$\sqrt {2}$≈566(米),
答:直线l上距离D点566米的C处开挖.
点评:
此题主要考查了勾股定理的应用,在应用勾股定理解决实际问题时勾股定理与方程的结合是解决实际问题常用的方法,关键是从题中抽象出勾股定理这一数学模型,画出准确的示意图.领会数形结合的思想的应用.
2单选题
如图,在Rt△ABC中,∠ACB=60°,DE是斜边AC的中垂线,分别交AB、AC于D、E两点.若BD=2,则AC的长是( )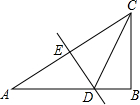
题目答案
您的答案
答案解析
分析:
已知∠ACB,根据线段垂直平分线求出AD=CD,求出∠ACD、∠DCB,求出CD、AD、AB,由勾股定理求出BC,再求出AC即可.
解答:
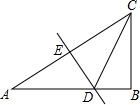
解:如图,∵在Rt△ABC中,∠ACB=60°,
∴∠A=30°.
∵DE垂直平分斜边AC,
∴AD=CD,
∴∠ACD=∠A=30°,
∴∠DCB=60°-30°=30°,
∵BD=2,
∴AD=CD=2BD=4,
∴AB=4+2=6,
在△BCD中,由勾股定理得:BC=2$\sqrt {3}$,
在△ABC中,由勾股定理得:AC=$\sqrt {}$=4$\sqrt {3}$,
故选:B.
点评:
本题考查了线段垂直平分线,含30°的直角三角形,等腰三角形的性质,三角形的内角和定理等知识点的应用,主要考查学生运用这些定理进行推理的能力,题目综合性比较强,难度适中.
3单选题
如图,在Rt△ABC中,∠ACB=90°,AD平分∠BAC与BC相交于点D,若AD=4,CD=2,则AB的长是{_ _}.
题目答案
您的答案
答案解析
分析:
先求出∠CAD=30°,求出∠BAC=60°,∠B=30°,根据勾股定理求出AC,再求出AB=2AC,代入求出即可.
解答:
解:∵在Rt△ACD中,∠C=90°,CD=2,AD=4,
∴∠CAD=30°,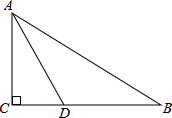
∴由勾股定理得:AC=$\sqrt {}$=2$\sqrt {3}$,
∵AD平分∠BAC,
∴∠BAC=60°,
∴∠B=30°,
∴AB=2AC=4$\sqrt {3}$,
故答案为:4$\sqrt {3}$,选A.
点评:
本题考查了含30度角的直角三角形性质,三角形内角和定理,勾股定理的应用,解此题的关键是求出AC长和求出∠B=30°,注意:在直角三角形中,如果有一个角等于30°,那么它所对的直角边等于斜边的一半.
4单选题
如图,Rt△ABC中,∠C=90°,∠B=30°,BC=6,则AB的长为___.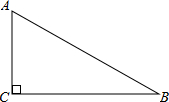
题目答案
您的答案
答案解析
分析:
利用30°的直角三角形中,三边从小到大的比是1:$\sqrt {3}$:2来得出解.
解答:
解:∵∠C=90°,∠B=30°,
∴AC:BC:AB=1:$\sqrt {3}$:2.
∵BC=6,
∴AB=4$\sqrt {3}$,
故答案为:4$\sqrt {3}$.
点评:
本题主要考察了30°的直角三角形中,三边从小到大的比是1:$\sqrt {3}$:2.
5单选题
已知△ABC为等边三角形,BD为中线,延长BC至E,使CE=CD=1,连接DE,则DE={_ _}.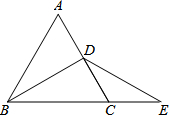
题目答案
您的答案
答案解析
分析:
根据等腰三角形和三角形外角性质求出BD=DE,求出BC,在Rt△BDC中,由勾股定理求出BD即可.
解答:
解:∵△ABC为等边三角形,
∴∠ABC=∠ACB=60°,AB=BC,
∵BD为中线,
∴∠DBC=$\frac {1}{2}$∠ABC=30°,
∵CD=CE,
∴∠E=∠CDE,
∵∠E+∠CDE=∠ACB,
∴∠E=30°=∠DBC,
∴BD=DE,
∵BD是AC中线,CD=1,
∴AD=DC=1,
∵△ABC是等边三角形,
∴BC=AC=1+1=2,BD⊥AC,
在Rt△BDC中,由勾股定理得:BD=$\sqrt {}$=$\sqrt {3}$,
即DE=BD=$\sqrt {3}$,
故答案为:$\sqrt {3}$,选B.
点评:
本题考查了等边三角形性质,勾股定理,等腰三角形性质,三角形的外角性质等知识点的应用,关键是求出DE=BD和求出BD的长.
6单选题
如图,若∠A=60°,AC=20m,则BC大约是(结果精确到0.1m) ( )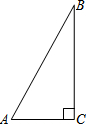
题目答案
您的答案
答案解析
分析:
首先计算出∠B的度数,再根据直角三角形的性质可得AB=40m,再利用勾股定理计算出BC长即可.
解答:
解:∵∠A=60°,∠C=90°,
∴∠B=30°,
∴AB=2AC,
∵AC=20m,
∴AB=40m,
∴BC=$\sqrt {}$=$\sqrt {1600-400}$=$\sqrt {1200}$=20$\sqrt {3}$≈34.6(m),
故选:B.
点评:
此题主要考查了勾股定理,以及直角三角形的性质,关键是掌握在直角三角形中,30°角所对的直角边等于斜边的一半.在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方.
7单选题
如图,在Rt△ABC中,∠BAC=90°,点D在BC边上,且△ABD是等边三角形.若AB=2,则△ABC的周长为{_ _}.(结果保留根号)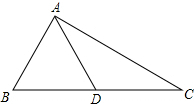
题目答案
您的答案
答案解析
分析:
根据等边三角形性质求出∠B=60°,求出∠C=30°,求出BC=4,根据勾股定理求出AC,相加即可求出答案.
解答:
解:∵△ABD是等边三角形,
∴∠B=60°,
∵∠BAC=90°,
∴∠C=180°-90°-60°=30°,
∵AB=2,
∴BC=2AB=4,
在Rt△ABC中,由勾股定理得:AC=$\sqrt {}$=$\sqrt {}$=2$\sqrt {3}$,
∴△ABC的周长是AC+BC+AB=2$\sqrt {3}$+4+2=6+2$\sqrt {3}$.
答:△ABC的周长是6+2$\sqrt {3}$,选C.
点评:
本题考查了勾股定理,含30度角的直角三角形,等边三角形性质,三角形的内角和定理等知识点的应用,主要培养学生运用性质进行推理和计算的能力,此题综合性比较强,是一道比较好的题目.
8单选题
如图,△ABC是等边三角形,P是∠ABC的平分线BD上一点,PE⊥AB于点E,线段BP的垂直平分线交BC于点F,垂足为点Q.若BF=2,则PE的长为( )
题目答案
您的答案
答案解析
分析:
先根据△ABC是等边三角形,P是∠ABC的平分线可知∠EBP=∠QBF=30°,再根据BF=2,FQ⊥BP可得出BQ的长,再由BP=2BQ可求出BP的长,在Rt△BEP中,根据∠EBP=30°即可求出PE的长.
解答:
解:∵△ABC是等边三角形,P是∠ABC的平分线,
∴∠EBP=∠QBF=30°,
∵BF=2,QF为线段BP的垂直平分线,
∴∠FQB=90°,
∴QF=$\frac {1}{2}$BF=1,BQ=$\sqrt {3}$QF=$\sqrt {3}$,
∴BP=2BQ=2$\sqrt {3}$,
在Rt△BEP中,
∵∠EBP=30°,
∴PE=$\frac {1}{2}$BP=$\sqrt {3}$.
故选C.
点评:
本题考查的是等边三角形的性质、角平分线的性质及直角三角形的性质,熟知等边三角形的三个内角都是60°是解答此题的关键.
9单选题
如图,在Rt△ABC中,∠A=30°,DE垂直平分斜边AC,交AB于D,E是垂足,连接CD,若BD=1,则AC的长是( )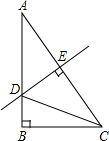
题目答案
您的答案
答案解析
分析:
求出∠ACB,根据线段垂直平分线求出AD=CD,求出∠ACD、∠DCB,求出CD、AD、AB,由勾股定理求出BC,再求出AC即可.
解答:
解:∵∠A=30°,∠B=90°,
∴∠ACB=90°-30°=60°,
∵DE垂直平分斜边AC,
∴AD=CD,
∴∠ACD=∠A=30°,
∴∠DCB=60°-30°=30°,
∵BD=1,
∴AD=CD=2BD=2,
∴AB=1+2=3,
在△BCD中,由勾股定理得:BC=$\sqrt {3}$,
在△ABC中,AC=2BC=2$\sqrt {3}$,
故选A.
点评:
本题考查了线段垂直平分线,含30°的直角三角形,等腰三角形的性质,三角形的内角和定理等知识点的应用,主要考查学生运用这些定理进行推理的能力,题目综合性比较强,难度适中.
10单选题
如图,△ABC和△DCE都是边长为4的等边三角形,点B、C、E在同一条直线上,连接BD,则BD的长为( )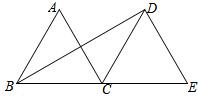
题目答案
您的答案
答案解析
分析:
根据等边三角形的性质、等腰三角形的性质和三角形的外角的性质可以发现∠BDE=90°,再进一步根据勾股定理进行求解.
解答:
解:∵△ABC和△DCE都是边长为4的等边三角形,
∴∠DCE=∠CDE=60°,BC=CD=4.
∴∠BDC=∠CBD=30°.
∴∠BDE=90°.
∴BD=$\sqrt {}$=4$\sqrt {3}$.
故选D.
点评:
此题综合应用了等边三角形的性质、等腰三角形的性质、三角形的外角的性质和勾股定理.
11单选题
如图,在△ABC中,∠C=90°,∠B=22.5°,AB的垂直平分线交AB于D,交BC于E,若CE=3,则BE的长是( )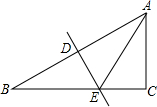
题目答案
您的答案
答案解析
分析:
利用线段的垂直平分线的性质计算.
解答:
解:已知∠C=90°,∠B=22.5°,DE垂直平分AB.
故∠EAB=∠B=22.5°,
∴∠AEC=45°.
又∵∠C=90°,
∴△ACE为等腰直角三角形,
∴AC=CE=3,
根据勾股定理得AE=3$\sqrt {2}$.
∴BE=AE=3$\sqrt {2}$,故选D.
点评:
本题考查的是线段的垂直平分线的性质(垂直平分线上任意一点,和线段两端点的距离相等),难度一般.
12单选题
如图,在边长为1的等边△ABC中,中线AD与中线BE相交于点O,则OA长度为( )
题目答案
您的答案
答案解析
分析:
根据等边三角形三线合一的特点及直角三角形的性质解答即可.
解答:
解:∵△ABC是等边三角形,AD、BE为中线;
∴BD=AE=$\frac {1}{2}$,∠ABE=∠BAD=30°,∠AEB=∠ADB=90°;
∴AD=BE=$\frac {$\sqrt {3}$}{2}$;
在Rt△BOD中,BD=$\frac {1}{2}$,∠DBO=30°;
∴OD=$\frac {BD}{$\sqrt {3}$}$=$\frac {$\sqrt {3}$}{6}$;
∴OA=AD-OD=$\frac {$\sqrt {3}$}{2}$-$\frac {$\sqrt {3}$}{6}$=$\frac {$\sqrt {3}$}{3}$.
故OA的长度为$\frac {$\sqrt {3}$}{3}$,选A.
点评:
此题比较简单,解答此题的关键是熟知等边三角形三线合一的性质.
13填空题
如图所示,点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别是C、D,若OE=4,∠AOB=60°,则DE=.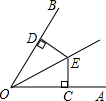
题目答案
您的答案
答案解析
分析:
利用角平分线的性质计算.
解答:
解:∵OE平分∠AOB
∴∠DOE=30°
∴DE=$\frac {1}{2}$OE=$\frac {1}{2}$×4=2.
点评:
本题主要考查平分线的性质和直角三角形的性质.
14单选题
等腰直角三角形的三边之比为( )
题目答案
您的答案
答案解析
分析:
先设等腰直角三角形的一个直角边长为a,根据勾股定理计算出其斜边的长,然后三边相比即可.
解答:
解:设等腰直角三角形的一个直角边长为a,
则另一边长也为a,其斜边长为$\sqrt {}$=$\sqrt {2}$a,
所以等腰直角三角形的三边之比为a:a:$\sqrt {2}$a=1:1:$\sqrt {2}$.
故选B.
点评:
本题考查学生对等腰直角三角形和勾股定理的理解和掌握,解得此题的关键是利用勾股定理求出其斜边的长,此题难度不大,是一道基础题.
15单选题
如果一个三角形的三边之比为1:$\sqrt {2}$:1,那么最小边所对的角为( )
题目答案
您的答案
答案解析
分析:
根据勾股定理的逆定理进行解答即可.
解答:
解:设三角形的三边分别为x、$\sqrt {2}$x、x,
∴x+x_=($\sqrt {2}$x)_,
∴此三角形为直角三角形,
∴最大角为90°,
∵三边的比为1:$\sqrt {2}$:1,
∴此三角形为等腰直角三角形,
∴最小角为45°.
故选B.
点评:
本题考查的是等腰直角三角形的知识及勾股定理的逆定理,即若一个三角形的三边满足a_+b_=c_,则这个三角形是直角三角形.
16单选题
一个等腰直角三角形的斜边为 4$\sqrt {2}$,则其面积为( )
题目答案
您的答案
答案解析
分析:
设等腰直角三角形的两直角边为x,由勾股定理得出方程x+x_=(4$\sqrt {2}$)_,求出x,再根据三角形的面积公式求出即可.
解答:
解:设等腰直角三角形的两直角边为x,
则由勾股定理得:x+x_=(4$\sqrt {2}$)_,
解得:x=4,
即等腰直角三角形的面积是:$\frac {1}{2}$×4×4=8,
故选B.
点评:
本题考查了等腰直角三角形性质、勾股定理、三角形的面积等知识点,关键是求出等腰直角三角形的直角边,用了方程思想.
17单选题
如果一个等腰直角三角形的面积为2,则斜边长为( )
题目答案
您的答案
答案解析
分析:
先设等腰直角三角形一个直角边为x,利用等腰直角三角形的面积为2,求出等腰直角三角形一个直角边,再用勾股定理即可求出其斜边的长.
解答:
解:设等腰直角三角形一个直角边为x,
则x×x×$\frac {1}{2}$=2,解得x=2,
由勾股定理得斜边长为2$\sqrt {2}$.
故选C.
点评:
此题考查学生对等腰直角三角形和勾股定理的理解和掌握,解答此题的关键是先求出等腰直角三角形一个直角边的长,这是此题的突破点,难度不大,是一道基础题.
18单选题
如图,△ABC中,∠ACB=90°,∠A=45°,AC=6,则AB边上的高CD为( ).
题目答案
您的答案
答案解析
分析:
由已知直角三角形ABC中,∠ACB=90°,∠A=45°,CD是AB边上的高可结合等腰直角三角形的性质得到CD的值.
解答:
解:∵∠ACB=90°,∠A=45°,
∴∠B=45°,
∴AC=BC,
∵AC=6,
∴AB=$\sqrt {2}$AC=6$\sqrt {2}$,
又∵CD⊥AB,
∴AD=BD=$\frac {1}{2}$AB=3$\sqrt {2}$,
∴CD=AD=3$\sqrt {2}$,选C.
点评:
本题主要考查了等腰直角三角形的性质,熟记性质是解题的关键.