- 有理数(I)有理数(I)
- 正数与负数正数与负数
- 有理数的概念有理数的概念
- 有理数的分类有理数的分类
- 数轴数轴
- 相反数相反数
- 绝对值绝对值
- 绝对值非负性绝对值非负性
- 有理数比较大小有理数比较大小
- 有理数(II)有理数(II)
- 有理数的加法有理数的加法
- 减法及加减法混合运算减法及加减法混合运算
- 有理数凑整巧算有理数凑整巧算
- 有理数的乘法有理数的乘法
- 除法及乘除混合运算除法及乘除混合运算
- 有理数的四则混合运算有理数的四则混合运算
- 利用乘法分配律巧算利用乘法分配律巧算
- 有理数的乘方有理数的乘方
- 有理数的混合运算有理数的混合运算
- 科学记数法与近似数科学记数法与近似数
- 整式的加减整式的加减
- 用含字母的式子表示数用含字母的式子表示数
- 单项式单项式
- 多项式多项式
- 同类项同类项
- 整式的概念与方程综合整式的概念与方程综合
- 整式的加减整式的加减
- 整式化简之与某项无关整式化简之与某项无关
- 整式的化简与求值整式的化简与求值
- 利用特殊概念化简求值利用特殊概念化简求值
- 整体代入求值整体代入求值
- 加减两个已知式求未知式加减两个已知式求未知式
- 绝对值与平方的非负性绝对值与平方的非负性
- 绝对值的化简绝对值的化简
- 数轴上数的比较与运算数轴上数的比较与运算
- 数轴背景下的绝对值化简数轴背景下的绝对值化简
- 一元一次方程(I)一元一次方程(I)
- 一元一次方程一元一次方程
- 等式的性质等式的性质
- 合并同类项与移项合并同类项与移项
- 去括号去括号
- 去分母去分母
- 解分母是小数的一次方程解分母是小数的一次方程
- 与数字有关的一元一次方程与数字有关的一元一次方程
- 与工程有关的一元一次方程与工程有关的一元一次方程
- 与经济有关的一元一次方程与经济有关的一元一次方程
- 与行程有关的一元一次方程与行程有关的一元一次方程
- 方案决策问题方案决策问题
- 一元一次方程(II)一元一次方程(II)
- 简单的绝对值方程简单的绝对值方程
- 恒等式的概念恒等式的概念
- 恒等式之特值法恒等式之特值法
- 已知方程的解求参数已知方程的解求参数
- 同解问题同解问题
- 系数含参的一元一次方程系数含参的一元一次方程
- 整数解问题整数解问题
- 几何图形初步(I)几何图形初步(I)
- 展开图初步展开图初步
- 立方体的展开图立方体的展开图
- 立方体相对两面立方体相对两面
- 展开图进阶展开图进阶
- 旋转体旋转体
- 直线射线线段的概念直线射线线段的概念
- 几何作图初步几何作图初步
- 两点之间线段最短两点之间线段最短
- 与线段有关的简单计算与线段有关的简单计算
- 线段计算之多解问题线段计算之多解问题
- 线段计算之列方程线段计算之列方程
- 双中点模型双中点模型
- 几何图形初步(II)几何图形初步(II)
- 角的概念角的概念
- 角度换算角度换算
- 角度的四则运算角度的四则运算
- 余角和补角余角和补角
- 余角和补角之列方程余角和补角之列方程
- 方向角方向角
- 角度计算之三角板问题角度计算之三角板问题
- 角度计算之双直角模型角度计算之双直角模型
- 角度计算之角平分线角度计算之角平分线
- 双角平分线模型双角平分线模型
- 角度计算之列方程角度计算之列方程
- 相交线与平行线相交线与平行线
- 相交线相交线
- 垂直垂直
- 垂线段最短垂线段最短
- 角度计算之多解问题角度计算之多解问题
- 同位角、内错角、同旁内角同位角、内错角、同旁内角
- 平行线及其判定平行线及其判定
- 平行线的性质平行线的性质
- 与平行线有关的计算与平行线有关的计算
- 平行线之M模型平行线之M模型
- 命题与定理命题与定理
- 平移平移
- 实数实数
- 平方根平方根
- 立方根立方根
- 实数的概念实数的概念
- 根号几的估算根号几的估算
- 根号几的精确估算根号几的精确估算
- 平面直角坐标系平面直角坐标系
- 平面直角坐标系的概念平面直角坐标系的概念
- 坐标系不同区域点的特点坐标系不同区域点的特点
- 点到坐标轴的距离点到坐标轴的距离
- 坐标系中点的平移坐标系中点的平移
- 坐标系中图形的平移坐标系中图形的平移
- 已知两点确定第三点的坐标已知两点确定第三点的坐标
- 二元一次方程组二元一次方程组
- 二元一次方程组的概念二元一次方程组的概念
- 代入消元法代入消元法
- 加减消元法加减消元法
- 解复杂的二元一次方程组解复杂的二元一次方程组
- 概念中的二元一次方程组概念中的二元一次方程组
- 二元一次方程组实际问题二元一次方程组实际问题
- 三元一次方程组的解法三元一次方程组的解法
- 已知方程(组)的解求参数已知方程(组)的解求参数
- 解常数项含参的方程组解常数项含参的方程组
- 消元消元
- 不等式与不等式组不等式与不等式组
- 不等式不等式
- 不等式的性质不等式的性质
- 解一元一次不等式解一元一次不等式
- 解一元一次不等式组解一元一次不等式组
- 不等式与坐标系综合不等式与坐标系综合
- 不等式的应用不等式的应用
- 解常数项含参的不等式解常数项含参的不等式
- 解系数含参的不等式解系数含参的不等式
- 含参不等式组含参不等式组
- 含参方程与不等式综合含参方程与不等式综合
- 含参方程组与不等式综合含参方程组与不等式综合
- 数据的收集、整理与描述数据的收集、整理与描述
- 统计调查统计调查
- 常见统计图常见统计图
- 直方图直方图
- 利用关键数据补全图表利用关键数据补全图表
- 三角形(I)三角形(I)
- 三角形的三边关系三角形的三边关系
- 利用三边关系计数利用三边关系计数
- 三角形按边分类三角形按边分类
- 三角形中的线段三角形中的线段
- 三角形内角和定理三角形内角和定理
- 三角形内角和之列方程三角形内角和之列方程
- 三角形按角度分类三角形按角度分类
- 三角形中的双垂直模型三角形中的双垂直模型
- 三角形的外角三角形的外角
- 三角形与平行线综合三角形与平行线综合
- 高线角平分线综合高线角平分线综合
- 三角形(II)三角形(II)
- 多边形初步多边形初步
- 多边形的对角线多边形的对角线
- 多边形的内角和多边形的内角和
- 多边形的外角和多边形的外角和
- 多边形的内角和进阶多边形的内角和进阶
- “8”字形和“A”字形“8”字形和“A”字形
- 燕尾形燕尾形
- 内角平分线的交角内角平分线的交角
- 内外角平分线的交角内外角平分线的交角
- 全等三角形全等三角形
- 全等三角形的概念和性质全等三角形的概念和性质
- 全等三角形的判定(SSS)全等三角形的判定(SSS)
- 全等三角形的判定(SAS)全等三角形的判定(SAS)
- 全等三角形的判定(ASA)全等三角形的判定(ASA)
- 全等三角形的判定(HL)全等三角形的判定(HL)
- 全等三角形判定综合全等三角形判定综合
- 证了全等再说证了全等再说
- 角平分线的性质与判定角平分线的性质与判定
- 多次证明全等多次证明全等
- 三垂直模型三垂直模型
- 轴对称(I)轴对称(I)
- 轴对称基本概念和性质轴对称基本概念和性质
- 垂直平分线的性质与判定垂直平分线的性质与判定
- 垂直平分线作图问题垂直平分线作图问题
- 画轴对称图形画轴对称图形
- 将军饮马问题将军饮马问题
- 将军饮马问题的应用将军饮马问题的应用
- 多次对称确定最短路径多次对称确定最短路径
- 等边对等角等边对等角
- 等边对等角多解问题等边对等角多解问题
- 等腰三角形三线合一等腰三角形三线合一
- 等角对等边等角对等边
- 角平分线+平行角平分线+平行
- 轴对称(II)轴对称(II)
- 两圆一中垂两圆一中垂
- 等边三角形等边三角形
- 含30°角的直角三角形含30°角的直角三角形
- 等边三角形类弦图模型等边三角形类弦图模型
- 绕直角顶点转90度绕直角顶点转90度
- 等腰共顶点模型等腰共顶点模型
- 连接两点连接两点
- 倍长中线倍长中线
- 角平分线对称性之作垂线角平分线对称性之作垂线
- 角平分线对称性之翻折角平分线对称性之翻折
- 角平分线对称性之顺延角平分线对称性之顺延
- 截长补短截长补短
- 整式的乘法与因式分解(I)整式的乘法与因式分解(I)
- 同底数幂的乘法同底数幂的乘法
- 幂的乘方幂的乘方
- 积的乘方积的乘方
- 整式的乘法整式的乘法
- 同底数幂的除法同底数幂的除法
- 整式的除法整式的除法
- 平方差公式平方差公式
- 完全平方公式完全平方公式
- 已知完全平方式求系数已知完全平方式求系数
- 整式的化简与求值整式的化简与求值
- 整式乘法的系数问题整式乘法的系数问题
- 降次法求值降次法求值
- 整式的乘法与因式分解(II)整式的乘法与因式分解(II)
- 因式分解的概念因式分解的概念
- 提公因式法提公因式法
- 公式法之平方差公式公式法之平方差公式
- 公式法之完全平方公式公式法之完全平方公式
- 分组分解法分组分解法
- 首一的十字相乘法首一的十字相乘法
- 非首一的十字相乘法非首一的十字相乘法
- 已知x、y的积与和求代数式的值已知x、y的积与和求代数式的值
- 利用因式分解求值利用因式分解求值
- 利用配方求值利用配方求值
- 分式分式
- 分式的基本概念分式的基本概念
- 分式值为0分式值为0
- 分式的基本性质分式的基本性质
- 约分与通分约分与通分
- 分式的乘除分式的乘除
- 分式的加减分式的加减
- 分式的混合运算分式的混合运算
- 分式的化简与求值分式的化简与求值
- 整数指数幂整数指数幂
- 解分式方程解分式方程
- 解含参分式方程解含参分式方程
- 含参分式方程增根问题含参分式方程增根问题
- 行程问题行程问题
- 工程问题工程问题
- 其它问题其它问题
- 二次根式二次根式
- 二次根式的概念二次根式的概念
- 二次根式的非负性二次根式的非负性
- 去根号法则去根号法则
- 二次根式乘除法法则二次根式乘除法法则
- 最简二次根式最简二次根式
- 二次根式的乘除运算二次根式的乘除运算
- 同类二次根式同类二次根式
- 二次根式的加减二次根式的加减
- 二次根式综合运算二次根式综合运算
- 含字母的根式化简含字母的根式化简
- 被开方数的非负性被开方数的非负性
- 条件有理化条件有理化
- 分母有理化分母有理化
- 复合二次根式化简复合二次根式化简
- 勾股定理勾股定理
- 利用勾股定理求边长利用勾股定理求边长
- 勾股定理多解问题勾股定理多解问题
- 特殊直角三角形特殊直角三角形
- 利用勾股定理列方程利用勾股定理列方程
- 最短路径问题最短路径问题
- 网格与勾股定理网格与勾股定理
- 勾股定理的逆定理勾股定理的逆定理
- 平行四边形平行四边形
- 平行四边形的性质(一)平行四边形的性质(一)
- 平行四边形的性质(二)平行四边形的性质(二)
- 性质反过来就是判定性质反过来就是判定
- 平行且相等平行且相等
- 判定方法辨析判定方法辨析
- 三角形中位线的性质三角形中位线的性质
- 矩形的性质矩形的性质
- 斜边中线定理斜边中线定理
- 矩形的判定(一)矩形的判定(一)
- 矩形的判定(二)矩形的判定(二)
- 菱形的性质菱形的性质
- 菱形的判定(一)菱形的判定(一)
- 菱形的判定(二)菱形的判定(二)
- 正方形的性质正方形的性质
- 与正方形有关的旋转全等与正方形有关的旋转全等
- 中点四边形中点四边形
- 梯形梯形
- 梯形的概念梯形的概念
- 等腰梯形的性质等腰梯形的性质
- 等腰梯形的判定等腰梯形的判定
- 梯形辅助线之平移腰梯形辅助线之平移腰
- 梯形辅助线之作双高梯形辅助线之作双高
- 梯形的中位线梯形的中位线
- 四边形判定的辨析四边形判定的辨析
- 一次函数(I)一次函数(I)
- 变量与函数变量与函数
- 自变量取值范围及解析式自变量取值范围及解析式
- 函数的表示方式函数的表示方式
- 函数的解析式与图象函数的解析式与图象
- 实际问题的函数图象实际问题的函数图象
- 正比例函数的概念正比例函数的概念
- 正比例函数的图象与性质正比例函数的图象与性质
- 求正比例函数解析式求正比例函数解析式
- 从正比例到一次函数从正比例到一次函数
- 一次函数图象的性质一次函数图象的性质
- 补全直线上点坐标补全直线上点坐标
- 待定系数法求解析式待定系数法求解析式
- 一次函数的上下平移一次函数的上下平移
- 平行直线k相同平行直线k相同
- 一次函数(II)一次函数(II)
- 直线与直线的交点直线与直线的交点
- 一次函数与方程一次函数与方程
- 一次函数与不等式一次函数与不等式
- 一次函数与坐标轴围成的面积一次函数与坐标轴围成的面积
- 数据的分析数据的分析
- 平均数平均数
- 中位数和众数中位数和众数
- 方差和极差方差和极差
- 一元二次方程(I)一元二次方程(I)
- 一元二次方程一元二次方程
- 直接开平方法直接开平方法
- 配方法配方法
- 公式法公式法
- 根的判别式根的判别式
- 十字相乘法十字相乘法
- 提取公因式法提取公因式法
- 根与系数的关系根与系数的关系
- 增长率问题增长率问题
- 篱笆问题篱笆问题
- 草坪问题草坪问题
- 分式方程应用题分式方程应用题
- 一元二次方程(II)一元二次方程(II)
- 利用方程根的概念求值利用方程根的概念求值
- 已知一个根求另一个根已知一个根求另一个根
- 已知根的个数求参数已知根的个数求参数
- 证明方程恒有实根证明方程恒有实根
- 整数根之判别式整数根之判别式
- 整数根之直接求根整数根之直接求根
- 根与系数的关系的应用根与系数的关系的应用
- 两根的倒数和两根的倒数和
- 两根之差的绝对值两根之差的绝对值
- 二次函数(I)二次函数(I)
- 最简二次函数的图象最简二次函数的图象
- 顶点式二次函数的图象顶点式二次函数的图象
- 从一般式到顶点式从一般式到顶点式
- 二次函数图象上点的性质二次函数图象上点的性质
- 求抛物线与坐标轴的交点求抛物线与坐标轴的交点
- 求二次函数的解析式求二次函数的解析式
- 顶点式和交点式顶点式和交点式
- 二次函数图象的平移1二次函数图象的平移1
- 二次函数图象的平移2二次函数图象的平移2
- 二次函数图象的变换二次函数图象的变换
- 二次函数特定范围内的最值二次函数特定范围内的最值
- 二次函数最值之解析式含参二次函数最值之解析式含参
- 看图象求参数关系看图象求参数关系
- 二次函数(II)二次函数(II)
- 用函数观点解方程1用函数观点解方程1
- 用函数观点解方程2用函数观点解方程2
- 用函数观点解不等式用函数观点解不等式
- 图象分析大杂烩图象分析大杂烩
- 利用二次函数求点坐标利用二次函数求点坐标
- 定价问题定价问题
- 利用二次函数求最值利用二次函数求最值
- 直线与抛物线的交点直线与抛物线的交点
- 看图写范围看图写范围
- 抛物线与直线的垂直距离抛物线与直线的垂直距离
- 旋转旋转
- 图形的旋转图形的旋转
- 旋转图形的画法旋转图形的画法
- 中心对称的概念中心对称的概念
- 旋转特殊角度旋转特殊角度
- 互补四边形半角模型1互补四边形半角模型1
- 互补四边形半角模型2互补四边形半角模型2
- 等腰直角三角形半角模型等腰直角三角形半角模型
- 圆(I)圆(I)
- 圆的基本概念圆的基本概念
- 垂径定理垂径定理
- 弧、弦、圆心角弧、弦、圆心角
- 圆周角圆周角
- 等弧对等角等弧对等角
- 直径对直角直径对直角
- 圆内接四边形圆内接四边形
- 圆中的特殊角圆中的特殊角
- 圆(II)圆(II)
- 点和圆的位置关系点和圆的位置关系
- 三角形外接圆三角形外接圆
- 直线和圆的位置关系直线和圆的位置关系
- 切线判定定理切线判定定理
- 切线性质定理切线性质定理
- 切线长定理切线长定理
- 圆和圆的位置关系圆和圆的位置关系
- 正多边形和圆正多边形和圆
- 弧长弧长
- 扇形面积扇形面积
- 圆锥圆锥
- 概率初步概率初步
- 随机事件随机事件
- 概率概率
- 用列举法求概率用列举法求概率
- 用频率估计概率用频率估计概率
- 反比例函数反比例函数
- 反比例函数的概念反比例函数的概念
- 反比例函数的图象反比例函数的图象
- 反比例函数的解析式反比例函数的解析式
- k的几何意义k的几何意义
- 实际问题与反比例函数实际问题与反比例函数
- 求交点求交点
- 用函数的观点解不等式用函数的观点解不等式
- 特殊的面积问题特殊的面积问题
- 相似相似
- 相似的概念相似的概念
- 平行线分线段成比例平行线分线段成比例
- 相似三角形的判定相似三角形的判定
- 相似三角形的性质相似三角形的性质
- 相似三角形应用举例相似三角形应用举例
- 位似的概念位似的概念
- 反A模型反A模型
- 射影定理射影定理
- 旋转相似模型旋转相似模型
- 共线三等角模型共线三等角模型
- 三角形内接正方形三角形内接正方形
- 角平分线定理角平分线定理
- 锐角三角函数锐角三角函数
- 锐角三角函数锐角三角函数
- 特殊角的三角函数特殊角的三角函数
- 解直角三角形解直角三角形
- 解直角三角形的应用解直角三角形的应用
- 双直角三角形及其应用双直角三角形及其应用
- 设未知数解直角三角形设未知数解直角三角形
- 利用已知角构造直角三角形利用已知角构造直角三角形
- 解梯形解梯形
- 解四边形解四边形
- 作垂线解三角形之SSA作垂线解三角形之SSA
- 投影与视图投影与视图
- 投影投影
- 三视图的概念三视图的概念
- 立方体堆的三视图立方体堆的三视图
《垂径定理》垂径定理
1填空题
如图AB是⊙O的直径,∠BAC=42°,点D是弦AC的中点,则∠DOC的度数是度.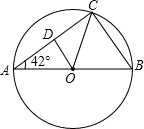
题目答案
您的答案
答案解析
分析:
根据点D是弦AC的中点,得到OD⊥AC,然后根据∠DOC=∠DOA即可求得答案.
解答:
∵AB是⊙O的直径,
∴OA=OC
∵∠A=42°
∴∠ACO=∠A=42°
∵D为AC的中点,
∴OD⊥AC,
∴∠DOC=90°-∠DCO=90°-42°=48°.
故答案为:48.
点评:
本题考查了垂径定理的知识,解题的关键是根的弦的中点得到弦的垂线.
2单选题
如图,AB是⊙O的直径,弦CD⊥AB,垂足为P.若CD=8,OP=3,则⊙O的半径为( )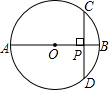
题目答案
您的答案
答案解析
分析:
连接OC,先根据垂径定理求出PC的长,再根据勾股定理即可得出OC的长.
解答:
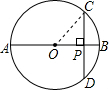 解:连接OC,
解:连接OC,
∵CD⊥AB,CD=8,
∴PC=$\frac {1}{2}$CD=$\frac {1}{2}$×8=4,
在Rt△OCP中,
∵PC=4,OP=3,
∴OC=PC_+OP_=4_+3_=5.
故选C.
点评:
本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.
3单选题
如图,AB是⊙O的直径,C是⊙O上一点,AB=10,AC=6,OD⊥BC,垂足是D,则BD的长为( )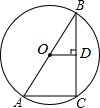
题目答案
您的答案
答案解析
分析:
由AB是⊙O的直径,可得∠C=90°,又由AB=10,AC=6,可求得BC的长,又由OD⊥BC,根据垂径定理的即可求得BD的长.
解答:
解:∵AB是⊙O的直径,
∴∠C=90°,
∵AB=10,AC=6,
∴BC=$\sqrt {}$=8,
∵OD⊥BC,
∴BD=$\frac {1}{2}$BC=4.
故选C.
点评:
此题考查了圆周角定理、垂径定理以及勾股定理.此题难度不大,注意掌握数形结合思想的应用.
4填空题
如图,在半径为13的⊙O中,OC垂直弦AB于点D,交⊙O于点C,AB=24,则CD的长是.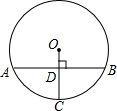
题目答案
您的答案
答案解析
分析:
连接OA,先根据垂径定理求出AD的长,再在Rt△AOD中利用勾股定理求出OD的长,进而可得出CD的长.
解答:
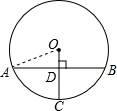 解:连接OA,
解:连接OA,
∵OC⊥AB,AB=24,
∴AD=$\frac {1}{2}$AB=12,
在Rt△AOD中,
∵OA=13,AD=12,
∴OD=$\sqrt {}$=$\sqrt {}$=5,
∴CD=OC-OD=13-5=8.
故答案为:8.
点评:
本题考查的是垂径定理及勾股定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.
5单选题
如图,AB是⊙O的直径,AB⊥CD于点E,若CD=6,则DE=( )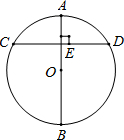
题目答案
您的答案
答案解析
分析:
直接根据垂径定理进行解答即可.
解答:
解:∵AB是⊙O的直径,AB⊥CD于点E,CD=6,
∴DE=$\frac {1}{2}$AB=$\frac {1}{2}$×6=3.
故选A.
点评:
本题考查的是垂径定理,即垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.
6填空题
如图,AB是⊙O的弦,AB长为8,P是⊙O上一个动点(不与A、B重合),过点O作OC⊥AP于点C,OD⊥PB于点D,则CD的长为.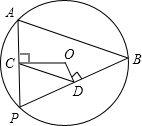
题目答案
您的答案
答案解析
分析:
根据垂径定理得出AC=PC,PD=BD,根据三角形的中位线推出CD=$\frac {1}{2}$AB,代入求出即可.
解答:
解:∵OC⊥AP,OD⊥PB,
∴由垂径定理得:AC=PC,PD=BD,
∴CD是△APB的中位线,
∴CD=$\frac {1}{2}$AB=$\frac {1}{2}$×8=4,
故答案为:4.
点评:
本题考查了三角形的中位线和垂径定理的应用,主要考查学生的推理能力,题目比较典型,难度适中.
7填空题
如图,AB是⊙O的弦,OC⊥AB于C.若AB=2$\sqrt {3}$,0C=1,则半径OB的长为.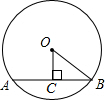
题目答案
您的答案
答案解析
分析:
先根据垂径定理得出BC的长,再在Rt△OBC中利用勾股定理求出OB的长即可.
解答:
解:∵AB是⊙O的弦,OC⊥AB于C,AB=2$\sqrt {3}$,
∴BC=$\frac {1}{2}$AB=$\sqrt {3}$
∵0C=1,
∴在Rt△OBC中,
OB=$\sqrt {}$=$\sqrt {}$=2.
故答案为:2.
点评:
本题考查的是垂径定理及勾股定理,先求出BC的长,再利用勾股定理求出OB的长是解答此题的关键.
8填空题
如图,AB、AC都是圆O的弦,OM⊥AB,ON⊥AC,垂足分别为M、N,如果MN=3,那么BC=.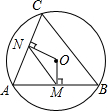
题目答案
您的答案
答案解析
分析:
由AB、AC都是圆O的弦,OM⊥AB,ON⊥AC,根据垂径定理可知M、N为AB、AC的中点,线段MN为△ABC的中位线,根据中位线定理可知BC=2MN.
解答:
∵AB、AC都是圆O的弦,OM⊥AB,ON⊥AC,
∴M、N为AB、AC的中点,即线段MN为△ABC的中位线,
∴BC=2MN=6.
故答案为:6.
点评:
本题考查了垂径定理,三角形的中位线定理的运用.关键是由垂径定理得出两个中点.
9单选题
如图,⊙O的直径AB=10cm,弦CD⊥AB,垂足为P.若OP:OB=3:5,则CD的长为( )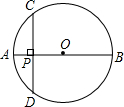
题目答案
您的答案
答案解析
分析:
根据⊙O的直径可得出半径OB的长,也就求出OP的长;连接OC,在Rt△OCP中,运用勾股定理可求出CP的长,进而可依据垂径定理求得CD的长.
解答:
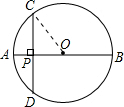 解:连接OC;
解:连接OC;
∵AB=10cm,∴OB=5cm;
∵OP:OB=3:5,∴OP=3cm;
Rt△OCP中,OC=OB=5cm,OP=3cm;
由勾股定理,得:CP=$\sqrt {}$=4cm;
所以CD=2PC=8cm,
故选C.
点评:
此题主要考查的是勾股定理及垂径定理的应用.
10单选题
如图,直线与两个同心圆分别相交于图示的各点,则正确的是( )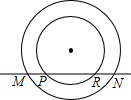
题目答案
您的答案
答案解析
分析:
作弦的弦心距,综合运用垂径定理和等式的性质进行证明.
解答:
 解:作OA⊥MN于A.
解:作OA⊥MN于A.
∵OA⊥MN,
∴MA=NA,PA=RA.
∴MP=RN.
故选B.
点评:
注意此题中的辅助线,同时作了两条弦的弦心距,熟练运用垂径定理.
11单选题
如图,已知⊙O的直径AB⊥弦CD于点E,下列结论中一定正确的是( )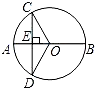
题目答案
您的答案
答案解析
分析:
根据垂径定理,即垂直于弦的直径平分弦即可判断.
解答:
∵⊙O的直径AB⊥弦CD,
∴CE=DE.
故选B.
点评:
本题考查了垂径定理,即垂直于弦的直径平分弦.
12填空题
如图,⊙O的半径OA=10cm,设AB=16cm,P为AB上一动点,则点P到圆心O的最短距离为cm.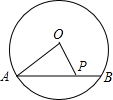
题目答案
您的答案
答案解析
分析:
根据垂线段最短,可以得到当OP⊥AB时,点P到圆心O的距离最短.根据垂径定理和勾股定理即可求解.
解答:
解:根据垂线段最短知,
当点P运动到OP⊥AB时,点P到到点O的距离最短,
由垂径定理知,此时点P为AB中点,AP=8cm,
由勾股定理得,此时OP=$\sqrt {}$=6cm.
点评:
本题利用了垂线段最短和垂径定理及勾股定理求解.
13单选题
如图,某公园的一座石拱桥是圆弧形(劣弧),其跨度为24米,拱的半径为13米,则拱高为( )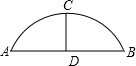
题目答案
您的答案
答案解析
分析:
先构建直角三角形,再利用勾股定理和垂径定理计算.
解答:
 解:因为跨度AB=24m,拱所在圆半径为13m,
解:因为跨度AB=24m,拱所在圆半径为13m,
所以找出圆心O并连接OA,延长CD到O,构成直角三角形,
利用勾股定理和垂径定理求出DO=5,
进而得拱高CD=CO-DO=13-5=8.故选B.
点评:
本题主要考查直角三角形和垂径定理的应用.
14单选题
在圆O中,圆O的半径为5cm,圆心O到弦AB的距离为4cm,则弦AB的长为( )
题目答案
您的答案
答案解析
分析:
连接圆心和弦的一端,通过构建直角三角形来求得弦AB的长.
解答:
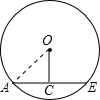 解:如图,连接OA;
解:如图,连接OA;
Rt△OAC中,OA=5cm,OC=4cm;
由勾股定理,得:AC=$\sqrt {}$=3cm;
∴AB=2AC=6cm;
故选D.
点评:
此题主要考查了勾股定理及垂径定理的综合应用能力.
15填空题
如图,AB、AC都是圆O的弦,OM⊥AB,ON⊥AC,垂足分别为M、N,如果BC=6,那么MN=.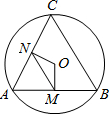
题目答案
您的答案
答案解析
分析:
由OM垂直于AB,ON垂直于AC,利用垂径定理得到M与N分别为AB、AC的中点,即MN为三角形ABC的中位线,利用中位线定理得到MN等于BC的一半,即可求出MN的长.
解答:
解:∵OM⊥AB,ON⊥AC,
∴M、N分别为AB、AC的中点,
∴MN为△ABC的中位线,
∵BC=6,
∴MN=$\frac {1}{2}$BC=3.
故答案为:3.
点评:
此题考查了垂径定理,以及中位线定理,熟练掌握定理是解本题的关键.
16单选题
如图,两个以O为圆心的同心圆,大圆的弦AB交小圆于C,D两点.OH⊥AB于H,则图中相等的线段共有( )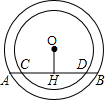
题目答案
您的答案
答案解析
分析:
根据垂径定理求解.
解答:
解:由垂径定理知,点H是AB的中点,也是CD的中点,则有CH=HD,AH=HB,所以AD=BC,AC=BD.
所以共有4组相等的线段.
故选D.
点评:
本题利用了垂径定理:垂直于弦的直径平分这条弦,并且平分这条弦所对的两段弧.