- 有理数(I)有理数(I)
- 正数与负数正数与负数
- 有理数的概念有理数的概念
- 有理数的分类有理数的分类
- 数轴数轴
- 相反数相反数
- 绝对值绝对值
- 绝对值非负性绝对值非负性
- 有理数比较大小有理数比较大小
- 有理数(II)有理数(II)
- 有理数的加法有理数的加法
- 减法及加减法混合运算减法及加减法混合运算
- 有理数凑整巧算有理数凑整巧算
- 有理数的乘法有理数的乘法
- 除法及乘除混合运算除法及乘除混合运算
- 有理数的四则混合运算有理数的四则混合运算
- 利用乘法分配律巧算利用乘法分配律巧算
- 有理数的乘方有理数的乘方
- 有理数的混合运算有理数的混合运算
- 科学记数法与近似数科学记数法与近似数
- 整式的加减整式的加减
- 用含字母的式子表示数用含字母的式子表示数
- 单项式单项式
- 多项式多项式
- 同类项同类项
- 整式的概念与方程综合整式的概念与方程综合
- 整式的加减整式的加减
- 整式化简之与某项无关整式化简之与某项无关
- 整式的化简与求值整式的化简与求值
- 利用特殊概念化简求值利用特殊概念化简求值
- 整体代入求值整体代入求值
- 加减两个已知式求未知式加减两个已知式求未知式
- 绝对值与平方的非负性绝对值与平方的非负性
- 绝对值的化简绝对值的化简
- 数轴上数的比较与运算数轴上数的比较与运算
- 数轴背景下的绝对值化简数轴背景下的绝对值化简
- 一元一次方程(I)一元一次方程(I)
- 一元一次方程一元一次方程
- 等式的性质等式的性质
- 合并同类项与移项合并同类项与移项
- 去括号去括号
- 去分母去分母
- 解分母是小数的一次方程解分母是小数的一次方程
- 与数字有关的一元一次方程与数字有关的一元一次方程
- 与工程有关的一元一次方程与工程有关的一元一次方程
- 与经济有关的一元一次方程与经济有关的一元一次方程
- 与行程有关的一元一次方程与行程有关的一元一次方程
- 方案决策问题方案决策问题
- 一元一次方程(II)一元一次方程(II)
- 简单的绝对值方程简单的绝对值方程
- 恒等式的概念恒等式的概念
- 恒等式之特值法恒等式之特值法
- 已知方程的解求参数已知方程的解求参数
- 同解问题同解问题
- 系数含参的一元一次方程系数含参的一元一次方程
- 整数解问题整数解问题
- 几何图形初步(I)几何图形初步(I)
- 展开图初步展开图初步
- 立方体的展开图立方体的展开图
- 立方体相对两面立方体相对两面
- 展开图进阶展开图进阶
- 旋转体旋转体
- 直线射线线段的概念直线射线线段的概念
- 几何作图初步几何作图初步
- 两点之间线段最短两点之间线段最短
- 与线段有关的简单计算与线段有关的简单计算
- 线段计算之多解问题线段计算之多解问题
- 线段计算之列方程线段计算之列方程
- 双中点模型双中点模型
- 几何图形初步(II)几何图形初步(II)
- 角的概念角的概念
- 角度换算角度换算
- 角度的四则运算角度的四则运算
- 余角和补角余角和补角
- 余角和补角之列方程余角和补角之列方程
- 方向角方向角
- 角度计算之三角板问题角度计算之三角板问题
- 角度计算之双直角模型角度计算之双直角模型
- 角度计算之角平分线角度计算之角平分线
- 双角平分线模型双角平分线模型
- 角度计算之列方程角度计算之列方程
- 相交线与平行线相交线与平行线
- 相交线相交线
- 垂直垂直
- 垂线段最短垂线段最短
- 角度计算之多解问题角度计算之多解问题
- 同位角、内错角、同旁内角同位角、内错角、同旁内角
- 平行线及其判定平行线及其判定
- 平行线的性质平行线的性质
- 与平行线有关的计算与平行线有关的计算
- 平行线之M模型平行线之M模型
- 命题与定理命题与定理
- 平移平移
- 实数实数
- 平方根平方根
- 立方根立方根
- 实数的概念实数的概念
- 根号几的估算根号几的估算
- 根号几的精确估算根号几的精确估算
- 平面直角坐标系平面直角坐标系
- 平面直角坐标系的概念平面直角坐标系的概念
- 坐标系不同区域点的特点坐标系不同区域点的特点
- 点到坐标轴的距离点到坐标轴的距离
- 坐标系中点的平移坐标系中点的平移
- 坐标系中图形的平移坐标系中图形的平移
- 已知两点确定第三点的坐标已知两点确定第三点的坐标
- 二元一次方程组二元一次方程组
- 二元一次方程组的概念二元一次方程组的概念
- 代入消元法代入消元法
- 加减消元法加减消元法
- 解复杂的二元一次方程组解复杂的二元一次方程组
- 概念中的二元一次方程组概念中的二元一次方程组
- 二元一次方程组实际问题二元一次方程组实际问题
- 三元一次方程组的解法三元一次方程组的解法
- 已知方程(组)的解求参数已知方程(组)的解求参数
- 解常数项含参的方程组解常数项含参的方程组
- 消元消元
- 不等式与不等式组不等式与不等式组
- 不等式不等式
- 不等式的性质不等式的性质
- 解一元一次不等式解一元一次不等式
- 解一元一次不等式组解一元一次不等式组
- 不等式与坐标系综合不等式与坐标系综合
- 不等式的应用不等式的应用
- 解常数项含参的不等式解常数项含参的不等式
- 解系数含参的不等式解系数含参的不等式
- 含参不等式组含参不等式组
- 含参方程与不等式综合含参方程与不等式综合
- 含参方程组与不等式综合含参方程组与不等式综合
- 数据的收集、整理与描述数据的收集、整理与描述
- 统计调查统计调查
- 常见统计图常见统计图
- 直方图直方图
- 利用关键数据补全图表利用关键数据补全图表
- 三角形(I)三角形(I)
- 三角形的三边关系三角形的三边关系
- 利用三边关系计数利用三边关系计数
- 三角形按边分类三角形按边分类
- 三角形中的线段三角形中的线段
- 三角形内角和定理三角形内角和定理
- 三角形内角和之列方程三角形内角和之列方程
- 三角形按角度分类三角形按角度分类
- 三角形中的双垂直模型三角形中的双垂直模型
- 三角形的外角三角形的外角
- 三角形与平行线综合三角形与平行线综合
- 高线角平分线综合高线角平分线综合
- 三角形(II)三角形(II)
- 多边形初步多边形初步
- 多边形的对角线多边形的对角线
- 多边形的内角和多边形的内角和
- 多边形的外角和多边形的外角和
- 多边形的内角和进阶多边形的内角和进阶
- “8”字形和“A”字形“8”字形和“A”字形
- 燕尾形燕尾形
- 内角平分线的交角内角平分线的交角
- 内外角平分线的交角内外角平分线的交角
- 全等三角形全等三角形
- 全等三角形的概念和性质全等三角形的概念和性质
- 全等三角形的判定(SSS)全等三角形的判定(SSS)
- 全等三角形的判定(SAS)全等三角形的判定(SAS)
- 全等三角形的判定(ASA)全等三角形的判定(ASA)
- 全等三角形的判定(HL)全等三角形的判定(HL)
- 全等三角形判定综合全等三角形判定综合
- 证了全等再说证了全等再说
- 角平分线的性质与判定角平分线的性质与判定
- 多次证明全等多次证明全等
- 三垂直模型三垂直模型
- 轴对称(I)轴对称(I)
- 轴对称基本概念和性质轴对称基本概念和性质
- 垂直平分线的性质与判定垂直平分线的性质与判定
- 垂直平分线作图问题垂直平分线作图问题
- 画轴对称图形画轴对称图形
- 将军饮马问题将军饮马问题
- 将军饮马问题的应用将军饮马问题的应用
- 多次对称确定最短路径多次对称确定最短路径
- 等边对等角等边对等角
- 等边对等角多解问题等边对等角多解问题
- 等腰三角形三线合一等腰三角形三线合一
- 等角对等边等角对等边
- 角平分线+平行角平分线+平行
- 轴对称(II)轴对称(II)
- 两圆一中垂两圆一中垂
- 等边三角形等边三角形
- 含30°角的直角三角形含30°角的直角三角形
- 等边三角形类弦图模型等边三角形类弦图模型
- 绕直角顶点转90度绕直角顶点转90度
- 等腰共顶点模型等腰共顶点模型
- 连接两点连接两点
- 倍长中线倍长中线
- 角平分线对称性之作垂线角平分线对称性之作垂线
- 角平分线对称性之翻折角平分线对称性之翻折
- 角平分线对称性之顺延角平分线对称性之顺延
- 截长补短截长补短
- 整式的乘法与因式分解(I)整式的乘法与因式分解(I)
- 同底数幂的乘法同底数幂的乘法
- 幂的乘方幂的乘方
- 积的乘方积的乘方
- 整式的乘法整式的乘法
- 同底数幂的除法同底数幂的除法
- 整式的除法整式的除法
- 平方差公式平方差公式
- 完全平方公式完全平方公式
- 已知完全平方式求系数已知完全平方式求系数
- 整式的化简与求值整式的化简与求值
- 整式乘法的系数问题整式乘法的系数问题
- 降次法求值降次法求值
- 整式的乘法与因式分解(II)整式的乘法与因式分解(II)
- 因式分解的概念因式分解的概念
- 提公因式法提公因式法
- 公式法之平方差公式公式法之平方差公式
- 公式法之完全平方公式公式法之完全平方公式
- 分组分解法分组分解法
- 首一的十字相乘法首一的十字相乘法
- 非首一的十字相乘法非首一的十字相乘法
- 已知x、y的积与和求代数式的值已知x、y的积与和求代数式的值
- 利用因式分解求值利用因式分解求值
- 利用配方求值利用配方求值
- 分式分式
- 分式的基本概念分式的基本概念
- 分式值为0分式值为0
- 分式的基本性质分式的基本性质
- 约分与通分约分与通分
- 分式的乘除分式的乘除
- 分式的加减分式的加减
- 分式的混合运算分式的混合运算
- 分式的化简与求值分式的化简与求值
- 整数指数幂整数指数幂
- 解分式方程解分式方程
- 解含参分式方程解含参分式方程
- 含参分式方程增根问题含参分式方程增根问题
- 行程问题行程问题
- 工程问题工程问题
- 其它问题其它问题
- 二次根式二次根式
- 二次根式的概念二次根式的概念
- 二次根式的非负性二次根式的非负性
- 去根号法则去根号法则
- 二次根式乘除法法则二次根式乘除法法则
- 最简二次根式最简二次根式
- 二次根式的乘除运算二次根式的乘除运算
- 同类二次根式同类二次根式
- 二次根式的加减二次根式的加减
- 二次根式综合运算二次根式综合运算
- 含字母的根式化简含字母的根式化简
- 被开方数的非负性被开方数的非负性
- 条件有理化条件有理化
- 分母有理化分母有理化
- 复合二次根式化简复合二次根式化简
- 勾股定理勾股定理
- 利用勾股定理求边长利用勾股定理求边长
- 勾股定理多解问题勾股定理多解问题
- 特殊直角三角形特殊直角三角形
- 利用勾股定理列方程利用勾股定理列方程
- 最短路径问题最短路径问题
- 网格与勾股定理网格与勾股定理
- 勾股定理的逆定理勾股定理的逆定理
- 平行四边形平行四边形
- 平行四边形的性质(一)平行四边形的性质(一)
- 平行四边形的性质(二)平行四边形的性质(二)
- 性质反过来就是判定性质反过来就是判定
- 平行且相等平行且相等
- 判定方法辨析判定方法辨析
- 三角形中位线的性质三角形中位线的性质
- 矩形的性质矩形的性质
- 斜边中线定理斜边中线定理
- 矩形的判定(一)矩形的判定(一)
- 矩形的判定(二)矩形的判定(二)
- 菱形的性质菱形的性质
- 菱形的判定(一)菱形的判定(一)
- 菱形的判定(二)菱形的判定(二)
- 正方形的性质正方形的性质
- 与正方形有关的旋转全等与正方形有关的旋转全等
- 中点四边形中点四边形
- 梯形梯形
- 梯形的概念梯形的概念
- 等腰梯形的性质等腰梯形的性质
- 等腰梯形的判定等腰梯形的判定
- 梯形辅助线之平移腰梯形辅助线之平移腰
- 梯形辅助线之作双高梯形辅助线之作双高
- 梯形的中位线梯形的中位线
- 四边形判定的辨析四边形判定的辨析
- 一次函数(I)一次函数(I)
- 变量与函数变量与函数
- 自变量取值范围及解析式自变量取值范围及解析式
- 函数的表示方式函数的表示方式
- 函数的解析式与图象函数的解析式与图象
- 实际问题的函数图象实际问题的函数图象
- 正比例函数的概念正比例函数的概念
- 正比例函数的图象与性质正比例函数的图象与性质
- 求正比例函数解析式求正比例函数解析式
- 从正比例到一次函数从正比例到一次函数
- 一次函数图象的性质一次函数图象的性质
- 补全直线上点坐标补全直线上点坐标
- 待定系数法求解析式待定系数法求解析式
- 一次函数的上下平移一次函数的上下平移
- 平行直线k相同平行直线k相同
- 一次函数(II)一次函数(II)
- 直线与直线的交点直线与直线的交点
- 一次函数与方程一次函数与方程
- 一次函数与不等式一次函数与不等式
- 一次函数与坐标轴围成的面积一次函数与坐标轴围成的面积
- 数据的分析数据的分析
- 平均数平均数
- 中位数和众数中位数和众数
- 方差和极差方差和极差
- 一元二次方程(I)一元二次方程(I)
- 一元二次方程一元二次方程
- 直接开平方法直接开平方法
- 配方法配方法
- 公式法公式法
- 根的判别式根的判别式
- 十字相乘法十字相乘法
- 提取公因式法提取公因式法
- 根与系数的关系根与系数的关系
- 增长率问题增长率问题
- 篱笆问题篱笆问题
- 草坪问题草坪问题
- 分式方程应用题分式方程应用题
- 一元二次方程(II)一元二次方程(II)
- 利用方程根的概念求值利用方程根的概念求值
- 已知一个根求另一个根已知一个根求另一个根
- 已知根的个数求参数已知根的个数求参数
- 证明方程恒有实根证明方程恒有实根
- 整数根之判别式整数根之判别式
- 整数根之直接求根整数根之直接求根
- 根与系数的关系的应用根与系数的关系的应用
- 两根的倒数和两根的倒数和
- 两根之差的绝对值两根之差的绝对值
- 二次函数(I)二次函数(I)
- 最简二次函数的图象最简二次函数的图象
- 顶点式二次函数的图象顶点式二次函数的图象
- 从一般式到顶点式从一般式到顶点式
- 二次函数图象上点的性质二次函数图象上点的性质
- 求抛物线与坐标轴的交点求抛物线与坐标轴的交点
- 求二次函数的解析式求二次函数的解析式
- 顶点式和交点式顶点式和交点式
- 二次函数图象的平移1二次函数图象的平移1
- 二次函数图象的平移2二次函数图象的平移2
- 二次函数图象的变换二次函数图象的变换
- 二次函数特定范围内的最值二次函数特定范围内的最值
- 二次函数最值之解析式含参二次函数最值之解析式含参
- 看图象求参数关系看图象求参数关系
- 二次函数(II)二次函数(II)
- 用函数观点解方程1用函数观点解方程1
- 用函数观点解方程2用函数观点解方程2
- 用函数观点解不等式用函数观点解不等式
- 图象分析大杂烩图象分析大杂烩
- 利用二次函数求点坐标利用二次函数求点坐标
- 定价问题定价问题
- 利用二次函数求最值利用二次函数求最值
- 直线与抛物线的交点直线与抛物线的交点
- 看图写范围看图写范围
- 抛物线与直线的垂直距离抛物线与直线的垂直距离
- 旋转旋转
- 图形的旋转图形的旋转
- 旋转图形的画法旋转图形的画法
- 中心对称的概念中心对称的概念
- 旋转特殊角度旋转特殊角度
- 互补四边形半角模型1互补四边形半角模型1
- 互补四边形半角模型2互补四边形半角模型2
- 等腰直角三角形半角模型等腰直角三角形半角模型
- 圆(I)圆(I)
- 圆的基本概念圆的基本概念
- 垂径定理垂径定理
- 弧、弦、圆心角弧、弦、圆心角
- 圆周角圆周角
- 等弧对等角等弧对等角
- 直径对直角直径对直角
- 圆内接四边形圆内接四边形
- 圆中的特殊角圆中的特殊角
- 圆(II)圆(II)
- 点和圆的位置关系点和圆的位置关系
- 三角形外接圆三角形外接圆
- 直线和圆的位置关系直线和圆的位置关系
- 切线判定定理切线判定定理
- 切线性质定理切线性质定理
- 切线长定理切线长定理
- 圆和圆的位置关系圆和圆的位置关系
- 正多边形和圆正多边形和圆
- 弧长弧长
- 扇形面积扇形面积
- 圆锥圆锥
- 概率初步概率初步
- 随机事件随机事件
- 概率概率
- 用列举法求概率用列举法求概率
- 用频率估计概率用频率估计概率
- 反比例函数反比例函数
- 反比例函数的概念反比例函数的概念
- 反比例函数的图象反比例函数的图象
- 反比例函数的解析式反比例函数的解析式
- k的几何意义k的几何意义
- 实际问题与反比例函数实际问题与反比例函数
- 求交点求交点
- 用函数的观点解不等式用函数的观点解不等式
- 特殊的面积问题特殊的面积问题
- 相似相似
- 相似的概念相似的概念
- 平行线分线段成比例平行线分线段成比例
- 相似三角形的判定相似三角形的判定
- 相似三角形的性质相似三角形的性质
- 相似三角形应用举例相似三角形应用举例
- 位似的概念位似的概念
- 反A模型反A模型
- 射影定理射影定理
- 旋转相似模型旋转相似模型
- 共线三等角模型共线三等角模型
- 三角形内接正方形三角形内接正方形
- 角平分线定理角平分线定理
- 锐角三角函数锐角三角函数
- 锐角三角函数锐角三角函数
- 特殊角的三角函数特殊角的三角函数
- 解直角三角形解直角三角形
- 解直角三角形的应用解直角三角形的应用
- 双直角三角形及其应用双直角三角形及其应用
- 设未知数解直角三角形设未知数解直角三角形
- 利用已知角构造直角三角形利用已知角构造直角三角形
- 解梯形解梯形
- 解四边形解四边形
- 作垂线解三角形之SSA作垂线解三角形之SSA
- 投影与视图投影与视图
- 投影投影
- 三视图的概念三视图的概念
- 立方体堆的三视图立方体堆的三视图
《用函数的观点解不等式》用函数的观点解不等式
1单选题
如图,在平面直角坐标系中,反比例函数y$_1$=$\frac {2}{x}$的图象与一次函数y$_2$=kx+b的图象交于A、B两点.若y$_1$<y$_2$,则x的取值范围是( )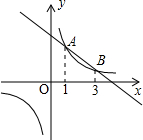
题目答案
您的答案
答案解析
分析:
当一次函数的值>反比例函数的值时,直线在双曲线的上方,直接根据图象写出一次函数的值>反比例函数的值x的取值范围,可得答案.
解答:
由图象可知,当x<0或1<x<3时,y$_1$<y$_2$,
故选:B.
点评:
本题考查了反比例函数与一函数的交点问题,反比例函数图象在下方的部分是不等的解.
2单选题
一次函数y=kx+b(k≠0)与反比例函数y=$\frac {k}{x}$ (k≠0)的图象在同一直角坐标系下的大致图象如图所示,则k、b的取值范围是( )
题目答案
您的答案
答案解析
分析:
本题需先判断出一次函数y=kx+b与反比例函数$\frac {k}{x}$ (k≠0)的图象在哪个象限内,再判断出k、b的大小即可.
解答:
解:∵一次函数y=kx+b的图象经过二、三、四象限,
∴k<0,b<0
又∵反比例函数$\frac {k}{x}$ (k≠0)的图象经过二、四象限,
∴k<0.
综上所述,k<0,b<0.
故选C.
点评:
本题主要考查了反比例函数和一次函数的交点问题,在解题时要注意图象在哪个象限内,是解题的关键.
3单选题
已知一次函数y$_1$=x-1和反比例函数y$_2$=$\frac {2}{x}$的图象在平面直角坐标系中交于A、B两点,当y$_1$>y$_2$时,x的取值范围是( )
题目答案
您的答案
答案解析
分析:
因为一次函数和反比例函数交于A、B两点,可知x-1=$\frac {2}{x}$,解得x=-1或x=2,进而可得A、B两点的坐标,据此,再结合函数解析式画图,据图可知当x>2时,以及当-1<x<0时,y$_1$>y$_2$.
解答:
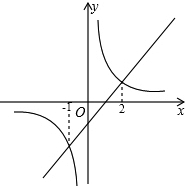 解:解方程x-1=$\frac {2}{x}$,得
解:解方程x-1=$\frac {2}{x}$,得
x=-1或x=2,
那么A点坐标是(-1,-2),B点坐标是(2,1),
如右图,
当x>2时,y$_1$>y$_2$,以及当-1<x<0时,y$_1$>y$_2$.
故选C.
点评:
本题考查了反比例函数与一次函数交点问题,解题的关键是能根据解析式画出函数的图象,并能根据图象解决问题.
4单选题
如图,反比例函数y$_1$=$\frac {k$_1$}{x}$的图象与正比例函数y$_2$=k$_2$x的图象交于点(2,1),则使y$_1$>y$_2$的x的取值范围是( )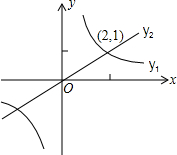
题目答案
您的答案
答案解析
分析:
先根据反比例函数与正比例函数的性质求出B点坐标,由函数图象即可得出结论.
解答:
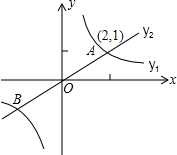 解:∵反比例函数与正比例函数的图象均关于原点对称,
解:∵反比例函数与正比例函数的图象均关于原点对称,
∴A、B两点关于原点对称,
∵A(2,1),
∴B(-2,-1),
∵由函数图象可知,当0<x<2或x<-2时函数y$_1$的图象在y$_2$的上方,
∴使y$_1$>y$_2$的x的取值范围是x<-2或0<x<2.
故选D.
点评:
本题考查的是反比例函数与一次函数的交点问题,能根据数形结合求出y$_1$>y$_2$时x的取值范围是解答此题的关键.
5单选题
一次函数y$_1$=kx+b(k≠0)与反比例函数y$_2$=$\frac {m}{x}$(m≠0),在同一直角坐标系中的图象如图所示,若y$_1$>y$_2$,则x的取值范围是( )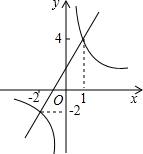
题目答案
您的答案
答案解析
分析:
先根据图象得出反比例函数与一次函数交点的坐标,再利用数形结合即可解答.
解答:
解:由函数图象可知一次函数y$_1$=kx+b与反比例函数y$_2$=$\frac {m}{x}$(m≠0)的交点坐标为(1,4),(-2,-2),
由函数图象可知,当-2<x<0或x>1时,y$_1$在y$_2$的上方,
∴当y$_1$>y$_2$时x的取值范围是-2<x<0或x>1.
故选A.
点评:
本题考查的是反比例函数与一次函数的交点问题,解答此题的关键是利用数形结合求出x的取值范围.
6单选题
一次函数y$_1$=k$_1$x+b和反比例函数y$_2$=$\frac {k$_2$}{x}$(k$_1$∙k$_2$≠0)的图象如图所示,若y$_1$>y$_2$,则x的取值范围是( )
题目答案
您的答案
答案解析
分析:
根据图象可以知道一次函数y$_1$=k$_1$x+b和反比例函数y$_2$=$\frac {k$_2$}{x}$(k$_1$∙k$_2$≠0)的图象的交点的横坐标,若y$_1$>y$_2$,则根据图象可以确定x的取值范围.
解答:
解:如图,依题意得一次函数y$_1$=k$_1$x+b和反比例函数y$_2$=$\frac {k$_2$}{x}$(k$_1$∙k$_2$≠0)的图象的交点的横坐标分别为x=-2或x=1,
若y$_1$>y$_2$,则y$_1$的图象在y$_2$的上面,
x的取值范围是-2<x<0或x>1.
故选A.
点评:
此题主要考查了反比例函数与一次函数的图象的交点问题,解题的关键是利用数形结合的方法解决问题.
7单选题
如图,函数y$_1$=x-1和函数y$_2$=$\frac {2}{x}$的图象相交于点M(2,m),N(-1,n),若y$_1$>y$_2$,则x的取值范围是( )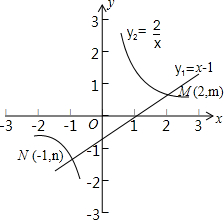
题目答案
您的答案
答案解析
分析:
根据反比例函数的自变量取值范围,y$_1$与y$_2$图象的交点横坐标,可确定y$_1$>y$_2$时,x的取值范围.
解答:
解:∵函数y$_1$=x-1和函数y$_2$=$\frac {2}{x}$的图象相交于点M(2,m),N(-1,n),
∴当y$_1$>y$_2$时,那么直线在双曲线的上方,
∴此时x的取值范围为-1<x<0或x>2.
故选D.
点评:
本题考查了反比例函数与一次函数的交点问题的运用.关键是根据图象的交点坐标,两个函数图象的位置确定自变量的取值范围.
8单选题
如图,直线y=kx+b经过A(-2,-1)和B(-3,0)两点,利用函数图象判断不等式$\frac {1}{x}$<kx+b的解集为( )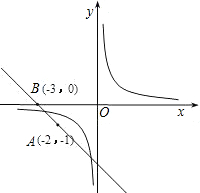
题目答案
您的答案
答案解析
分析:
直线y=kx+b经过A(-2,-1)和B(-3,0)两点,则利用待定系数法求得k,b的值,得到函数的解析式是y=-x-3,得到这个函数与y=$\frac {1}{x}$的交点的横坐标,再根据图象可以得到不等式$\frac {1}{x}$<kx+b的解集.
解答:
解:直线y=kx+b经过A(-2,-1)和B(-3,0)两点,
则$\left\{\begin{matrix}-2k+b=-1 \ -3k+b=0 \ \end{matrix}\right.$解得,解得$\left\{\begin{matrix}k=-1 \ b=-3 \ \end{matrix}\right.$,
因此函数的解析式是y=-x-3,
这个函数与y=$\frac {1}{x}$的交点的横坐标是$\frac {-3±$\sqrt {5}$}{2}$,
根据图象可以得到,不等式$\frac {1}{x}$<kx+b的解集为x<$\frac {-3-$\sqrt {5}$}{2}$或$\frac {-3+$\sqrt {5}$}{2}$<x<0.
故选D.
点评:
本题考查了一次函数与不等式(组)的关系及数形结合思想的应用.解决此类问题关键是仔细观察图形,注意几个关键点(交点、原点等),做到数形结合.