《直线方程的五种形式》直线方程的五种形式

1单选题

经过点A(-$\sqrt {3}$，3)且倾斜角为直线$\sqrt {3}$x+y+1=0的倾斜角的一半的直线方程是( )

$\sqrt {3}$x-y+6=0

$\sqrt {3}$x-y+7=0

2x+y-5=0

4x+3y+8=0

题目答案

答案解析

分析：

利用斜率与倾斜角的关系、直线的点斜式方程即可得出．

解答：

解：由直线$\sqrt {3}$x+y+1=0可得y=-$\sqrt {3}$x-1，设倾斜角为θ．

则斜率k=-$\sqrt {3}$，∴tanθ=-$\sqrt {3}$．

∴θ=120°．

∴要求的直线倾斜角为60°．

其斜率为$\sqrt {3}$．

∴要求的直线方程为：y-3=$\sqrt {3}$(x+$\sqrt {3}$)，

化为$\sqrt {3}$x-y+6=0．

故答案为：$\sqrt {3}$x-y+6=0，选A．

点评：

本题考查了斜率与倾斜角的关系、直线的点斜式方程，属于基础题．

2单选题

直线l经过点A(-2，2)并且和x轴的正半轴、y轴的正半轴所围成的三角形的面积是1，则该直线的方程为( )

x+3y-3=0

2x+3y-2=0

4x+3y-2=0

x+2y-2=0

题目答案

答案解析

分析：

直线的斜率存在，可设直线l的方程为：y-2=k(x+2)．分别令x=0，得y=2k+2；令y=0，解得x=-$\frac {2k+2}{k}$．由$\left\{\begin{matrix}2k+2＞0 \ -$\frac {2k+2}{k}$＞0 \ \end{matrix}\right.$，解得k的取值范围．再利用三角形的面积计算公式即可得出．

解答：

解：∵直线的斜率存在，

∴可设直线l的方程为：y-2=k(x+2)．

即y=kx+2k+2．

令x=0，得y=2k+2；令y=0，

解得x=-$\frac {2k+2}{k}$．

由$\left\{\begin{matrix}2k+2＞0 \ -$\frac {2k+2}{k}$＞0 \ \end{matrix}\right.$，解得-1＜k＜0．

∵S_△=1，

∴$\frac {1}{2}$(2k+2)(-$\frac {2k+2}{k}$)=1，

解得：k=-2或-$\frac {1}{2}$．

∵-1＜k＜0，∴k=-$\frac {1}{2}$．

∴直线l的方程为：x+2y-2=0，所以选D．

点评：

本题考查了直线的点斜式、三角形的面积计算公式，属于基础题．

3单选题

已知△ABC中，A(1，3)，AB、AC边上的中线所在直线方程分别为x-2y+1=0和y-1=0，则边BC所在直线方程为( )

x+2y-2=0

2x+3y-2=0

4x+3y-2=0

x-4y-1=0

题目答案

答案解析

分析：

由题意设B(x_B，1)，则AB的中点D($\frac {x_B+1}{2}$，2)，由D在中线CD可得$\frac {x_B+1}{2}$-2×2+1=0，解方程可得B(5，1)，同理可得C(-3，-1)，易得直线的方程．

解答：

解：由题意设B(x_B，1)，则AB的中点D($\frac {x_B+1}{2}$，2)

∵D在中线CD：x-2y+1=0上，∴$\frac {x_B+1}{2}$-2×2+1=0，

解得x_B=5，即B(5，1)．

同理∵点C在直线x-2y+1=0上，可以设C为(2y_C-1，y_C)，

由$\frac {y_C+3}{2}$=1可解得y_C=-1，即C(-3，-1)．

∴直线BC的方程为y-1=$\frac {-1-1}{-3-5}$(x-5)，

化为一般式可得x-4y-1=0，

故答案为：x-4y-1=0，选D．

点评：

本题考查直线的一般式方程，求出B和C的坐标是解决问题的关键，属基础题．

4单选题

倾斜角为135°，在y轴上的截距为-1的直线方程是（　　）

x-y+1=0

x-y-1=0

x+y-1=0

x+y+1=0

题目答案

答案解析

分析：

先求出直线的斜率，再利用在y轴上的截距是-1，用斜截式写出直线方程．

解答：

解：∵直线倾斜角是135°，

∴直线的斜率等于-1，

∵在y轴上的截距是-1，

由直线方程的斜截式得：y=-1•x-1，

即 y=-x-1，

故选D．

点评：

本题考查倾斜角与斜率的关系，用斜截式求直线的方程方法，解题的关键是正确把握截距的含义，属于基础题．

5单选题

已知直线的倾斜角为45°，在y轴上的截距为1，则此直线方程为（　　）

y=-x+1

y=x+1

y=-x-1

y=x-1

题目答案

答案解析

分析：

利用斜截式方程求解．

解答：

解：∵直线的倾斜角为45°，在y轴上的截距为1，

∴k=tan45°=1，

∴此直线方程为y=x+1．

故选：B．

点评：

本题考查直线方程的求法，注意斜截式方程的合理运用．

6单选题

直线$\frac {x}{a}$-$\frac {y}{b}$=1在y轴上的截距是（　　）

|b|

-b_

±b

题目答案

答案解析

分析：

要求直线与y轴的截距，方法是令x=0求出y的值即可．

解答：

解：令x=0，得：-$\frac {y}{b}$=1，

解得y=-b_．

故选B

点评：

此题比较容易，是一道基础题．学生只需知道截距的定义就可求出．

7单选题

在平面直角坐标系xOy中，已知点A(0，2)，B(-2，0)，C(1，0)，分别以△ABC的边AB，AC向外作正方形ABEF与ACGH，则直线FH的一般式方程为( )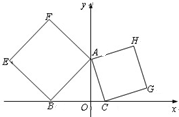

$\sqrt {3}$x-y+6=0

$\sqrt {3}$x-y+7=0

2x+y-5=0

x+4y-14=0

题目答案

答案解析

分析：

分别过H、F作y轴的垂线，垂足分别为M、N．根据正方形的性质证出Rt△AHM≌Rt△CAO，利用对应边相等及A、C两点的坐标，算出H(2，3)，同理得到F(-2，4)．由此算出直线FH的斜率，利用直线方程的点斜式列式，化简即可得到直线FH的一般式方程．

解答：

解：分别过H、F作y轴的垂线，垂足分别为M、N，

∵四边形ACGH为正方形，

∴Rt△AHM≌Rt△CAO，可得AM=OC，MH=OA，

∵A(0，2)，C(1，0)，

∴MH=OA=2，AM=OC=1，可得OM=OA+AM=3，

由此可得H坐标为(2，3)，同理得到F(-2，4)

∴直线FH的斜率为k=$\frac {4-3}{-2-2}$=-$\frac {1}{4}$，

可得直线FH的方程为y-3=-$\frac {1}{4}$(x-2)，化简得x+4y-14=0．

故答案为：D．

点评：

本题给出顶点A、B、C在坐标轴上的两个正方形ABEF与ACGH，在已知A、B、C的坐标情况下求直线FH的方程．着重考查了正方形的性质、全等三角形的判定与性质、直线的基本量与基本形式等知识，属于中档题．

8单选题

过点M(1，1)且倾斜角是直线2x-y=0的倾斜角的2倍的直线方程为（　　）

x-y=0

x+y-2=0

3x+4y-7=0

4x+3y-7=0

题目答案

答案解析

分析：

设直线2x-y=0的倾斜角为α，则过点M(1，1)要求的直线的倾斜角是2α．由直线2x-y=0可得y=2x，可得

tanα=2，利用tan2α=$\frac {2tanα}{1-tan_α}$即可得出要求的直线的斜率．

解答：

解：设直线2x-y=0的倾斜角为α，则过点M(1，1)要求的直线的倾斜角是2α．

由直线2x-y=0可得y=2x，∴tanα=2，

∴tan2α=$\frac {2tanα}{1-tan_α}$=$\frac {2×2}{1-2}$=-$\frac {4}{3}$．

∴要求的直线方程为y-1=-$\frac {4}{3}$(x-1)，化为4x+3y-7=0．

故选：D．

点评：

本题考查了直线的斜率与倾斜角之间的关系、正切的倍角公式，考查了计算能力，属于基础题．

9单选题

过点(-5，-4)作一直线l，使它与两坐标轴相交且与两轴所围成的三角形面积为5，则l的方程式为( )

3x-5y+20=0或4x-5y-8=0

3x-5y+20=0或2x-5y-10=0

8x-5y+20=0或4x-5y-8=0

8x-5y+20=0或2x-5y-10=0

题目答案

答案解析

分析：

如果设a，b分别表示l在x轴，y轴上的截距，则有$\frac {1}{2}$|a|•|b|=5，设出直线l的方程(点斜式)，求出a，b 的值，利用 $\frac {1}{2}$|a|•|b|=5，求得斜率，从而得到所求的直线方程．

解答：

解：设直线l方程为y+4=k(x+5)分别令y=0，x=0，

得l在x轴，y轴上截距为：a=$\frac {-5k+4}{k}$，b=5k-4，

由条件得ab=±10∴$\frac {-5k+4}{k}$•(5k-4)=±10

得25k_-30k+16=0无实数解；或25k_-50k+16=0，解得k$_1$=$\frac {8}{5}$，k$_2$=$\frac {2}{5}$

故所求的直线方程为：8x-5y+20=0或2x-5y-10=0，选D．

点评：

本题考查用待定系数法求直线方程，以及直线方程的一般式，直线在坐标轴上的截距的定义．

10单选题

过点P(1，3)且在x轴上的截距和在y轴上的截距相等的直线方程为（　　）

x+y-4=0

x+y-4=0或3x-y=0

x+y-4=0或3x+y=0

3x-y=0

题目答案

答案解析

分析：

分类讨论：当直线过原点时，可得斜率，可得方程，当直线不过原点时，设直线方程为$\frac {x}{a}$+$\frac {y}{a}$=1，代入点P(1，3)可得a的方程，解方程可得a值，可得直线的方程，整理为一般式即可．

解答：

解：当直线过原点时，斜率为$\frac {3-0}{1-0}$=3，故方程为y=3x，整理为一般式可得3x-y=0；当直线不过原点时，设直线方程为$\frac {x}{a}$+$\frac {y}{a}$=1，代入点P(1，3)可得$\frac {1}{a}$+$\frac {3}{a}$=1，解得a=4故直线方程为$\frac {x}{4}$+$\frac {y}{4}$=1，整理为一般式可得x+y-4=0，综上可得直线的方程为：3x-y=0或x+y-4=0故选：B

点评：

本题考查直线的截距式方程，涉及分类讨论的思想，属基础题．

11单选题

直线x+2y+1=0在y轴上的截距是（　　）

-1

$\frac {1}{2}$

-$\frac {1}{2}$

题目答案

答案解析

分析：

把直线的方程化为斜截式，即可得到直线在y轴上的截距．

解答：

解：直线x+2y+1=0 即 y=-$\frac {1}{2}$x-$\frac {1}{2}$，故直线在y轴上的截距为-$\frac {1}{2}$，

故选D．

点评：

本题主要考查直线在y轴上的截距的定义，直线的斜截式方程，属于基础题．

12单选题

已知直线的倾斜角为45°，在y轴上的截距为2，则此直线方程为（　　）

y=x+2

y=x-2

y=-x+2

y=-x-2

题目答案

答案解析

分析：

由题意可得直线的斜率和截距，由斜截式可得答案．

解答：

解：∵直线的倾斜角为45°，∴直线的斜率为k=tan45°=1，

由斜截式可得方程为：y=x+2，

故选A

点评：

本题考查直线的斜截式方程，属基础题．

13单选题

过点P(3，4)在两坐标轴上的截距都是非负整数的直线有多少条？（　　）

题目答案

答案解析

分析：

当直线经过原点时满足条件，直线方程为：y=$\frac {4}{3}$x．当直线不经过原点时，设直线方程为$\frac {x}{a}$+$\frac {y}{b}$=1，把点P(3，4)代入可得：$\frac {3}{a}$+$\frac {4}{b}$=1，对a，b取非负整数即可得出．

解答：

解：当直线经过原点时满足条件，直线方程为：y=$\frac {4}{3}$x．

当直线不经过原点时，设直线方程为$\frac {x}{a}$+$\frac {y}{b}$=1，

把点P(3，4)代入可得：$\frac {3}{a}$+$\frac {4}{b}$=1，

满足条件的a，b有(6，8)，(4，16)，(5，10)(9，6)，(15，5)，(7，7)．

综上可得：满足条件的直线共有7条．

故选：D．

点评：

本题考查了直线的截距式、整数的性质，考查了推理能力，属于基础题．

14单选题

过点A(0，1)，B(2，0)的直线的方程为( )

x+2y-2=0

2x+3y-2=0

4x+3y-2=0

x+3y-6=0

题目答案

答案解析

分析：

可根据两点的坐标求出直线的斜率，然后写出直线方程即可．

解答：

解：该直线的斜率k=$\frac {1-0}{0-2}$=-$\frac {1}{2}$，过(0，1)，

即可得到直线的方程为y-1=-$\frac {1}{2}$(x-0)，

化简得：x+2y-2=0，

故答案为A．

点评：

考查学生根据两点坐标会求直线的斜率，会写出直线的方程．

15填空题

直线l经过点P(1，-1)，且它的倾斜角是直线x-y+2=0的倾斜角的2倍，那么直线l的方程是x=．

填空题答案仅供参考

题目答案

答案解析

分析：

由已知得直线l过点P(1，-1)，倾斜角为90°，由此能求出直线l的方程．

解答：

解：∵直线l经过点P(1，-1)，且它的倾斜角是直线x-y+2=0的倾斜角的2倍，

直线x-y+2=0的斜率k=1，倾斜角为45°，

∴直线l过点P(1，-1)，倾斜角为90°，

∴直线l的方程为x=1．

故答案为：x=1．

点评：

本题考查直线方程的求法，是基础题，解题时要认真审题，注意直线方程的性质的合理运用．

16填空题

经过点 P(1，1)的直线在两坐标轴上的截距都是正数，若使截距之和最小，则该直线的方程是=0．

填空题答案仅供参考

题目答案

x+y-2

答案解析

分析：

设直线的截距式为：$\frac {x}{a}$+$\frac {y}{b}$=1(a，b＞0)，可得$\frac {1}{a}$+$\frac {1}{b}$=1．因此a+b=(a+b)($\frac {1}{a}$+$\frac {1}{b}$)=2+$\frac {b}{a}$+$\frac {a}{b}$，再利用基本不等式的性质即可得出．

解答：

解：设直线的截距式为：$\frac {x}{a}$+$\frac {y}{b}$=1(a，b＞0)，

则$\frac {1}{a}$+$\frac {1}{b}$=1．

∴a+b=(a+b)($\frac {1}{a}$+$\frac {1}{b}$)=2+$\frac {b}{a}$+$\frac {a}{b}$≥2+2$\sqrt {}$=4，当且仅当a=b=2时取等号．

∴该直线的方程是x+y-2=0．

故答案为：x+y-2=0．

点评：

本题考查了直线的截距式、基本不等式的性质，考查了推理能力与计算能力，属于中档题．

17填空题

已知直线l在y轴上的截距为-5，倾斜角的余弦值为$\frac {4}{5}$，则直线l的方程是．

填空题答案仅供参考

题目答案

答案解析

分析：

解答：

点评：

18填空题

过(0，4)，(-2，0)两点的直线的方程的一般式为=0．

填空题答案仅供参考

题目答案

2x-y+4

答案解析

分析：

根据所给点坐标的特点，可以用直线的截距式求直线方程，再化一般式即可．

解答：

解：因为直线过(0，4)，(-2，0)，

所以直线的方程为$\frac {x}{-2}$+$\frac {y}{4}$=1，

化为一般式为2x-y+4=0，

故答案为：2x-y+4=0．

点评：

本题考察直线方程的求解，属基础题．做题时要结合条件选对应的直线方程形式来求解．

19填空题

过(5，7)，(1，3)两点的直线方程为=0．

填空题答案仅供参考

题目答案

x-y+2

答案解析

分析：

根据两个点的坐标先求出直线的斜率，然后根据斜率和其中一点的坐标得到直线的方程即可．

解答：

解：设该直线的斜率为k，

因为直线过(5，7)和(1，3)所以k=$\frac {3-7}{1-5}$=1，

所以直线方程为y-3=1×(x-1)，化简得：x-y+2=0

故答案为：x-y+2=0．

点评：

考查学生会根据两个点的坐标求直线的两点式方程，以及根据两点的坐标会求过两点的斜率．

20填空题

过两点(1，2)和(3，4)的直线的方程为y=．

填空题答案仅供参考

题目答案

x+1

答案解析

分析：

根据两个点的坐标先求出直线的斜率，然后根据斜率和其中一点的坐标得到直线的方程即可．

解答：

解：设该直线的斜率为k，

因为直线过(1，2)和(3，4)所以k=$\frac {4-2}{3-1}$=1，

所以直线方程为y-2=1×(x-1)，化简得：y=x+1

故答案为y=x+1

点评：

考查学生会根据两个点的坐标求直线的两点式方程，以及根据两点的坐标会求过两点的斜率．

21单选题

过两点A(-1，2)，B(1，3)的直线方程为（　　）

x-2y+5=0

x+2y-3=0

2x-y+4=0

x+2y-7=0

题目答案

答案解析

分析：

由题意可得直线的两点式方程，化为一般式即可．

解答：

解：∵直线过两点A(-1，2)，B(1，3)，

∴直线的两点式方程为：$\frac {y-3}{2-3}$=$\frac {x-1}{-1-1}$，

化为一般式可得x-2y+5=0

故选：A

点评：

本题考查直线的两点式方程，属基础题．

读趣百科

《直线方程的五种形式》直线方程的五种形式

1单选题

题目答案

您的答案

答案解析

2单选题

题目答案

您的答案

答案解析

3单选题

题目答案

您的答案

答案解析

4单选题

题目答案

您的答案

答案解析

5单选题

题目答案

您的答案

答案解析

6单选题

题目答案

您的答案

答案解析

7单选题

题目答案

您的答案

答案解析

8单选题

题目答案

您的答案

答案解析

9单选题

题目答案

您的答案

答案解析

10单选题

题目答案

您的答案

答案解析

11单选题

题目答案

您的答案

答案解析

12单选题

题目答案

您的答案

答案解析

13单选题

题目答案

您的答案

答案解析

14单选题

题目答案

您的答案

答案解析

15填空题

题目答案

您的答案

答案解析

16填空题

题目答案

您的答案

答案解析

17填空题

题目答案

您的答案

答案解析

18填空题

题目答案

您的答案

答案解析

19填空题

题目答案

您的答案

答案解析

20填空题

题目答案